题目内容
(本小题满分14分)对于定义在区间D上的函数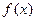 ,若存在闭区间
,若存在闭区间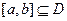 和常数
和常数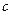 ,使得对任意
,使得对任意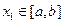 ,都有
,都有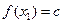 ,且对任意
,且对任意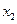 ∈D,当
∈D,当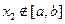 时,
时,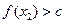 恒成立,则称函数
恒成立,则称函数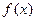 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数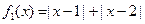 和
和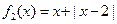 是否为R上的“平底
是否为R上的“平底 型”函数? 并说明理由;
型”函数? 并说明理由;
(Ⅱ)设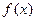 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式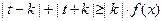 对一切
对一切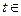 R恒成立,求实数
R恒成立,求实数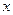 的取值范围;
的取值范围;
(Ⅲ)若函数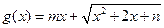 是区间
是区间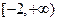 上的“平底型”函数,求
上的“平底型”函数,求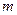 和
和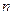 的值.
的值.
.
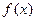 ,若存在闭区间
,若存在闭区间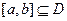 和常数
和常数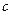 ,使得对任意
,使得对任意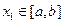 ,都有
,都有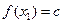 ,且对任意
,且对任意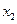 ∈D,当
∈D,当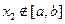 时,
时,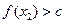 恒成立,则称函数
恒成立,则称函数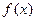 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.(Ⅰ)判断函数
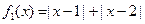 和
和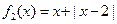 是否为R上的“平底
是否为R上的“平底 型”函数? 并说明理由;
型”函数? 并说明理由;(Ⅱ)设
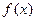 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式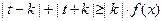 对一切
对一切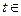 R恒成立,求实数
R恒成立,求实数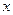 的取值范围;
的取值范围;(Ⅲ)若函数
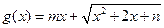 是区间
是区间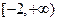 上的“平底型”函数,求
上的“平底型”函数,求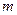 和
和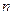 的值.
的值..
(1)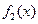 不是“平底型”函数(2)实数
不是“平底型”函数(2)实数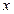 的范围是
的范围是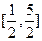 ⑶m=1,n=1
⑶m=1,n=1
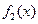 不是“平底型”函数(2)实数
不是“平底型”函数(2)实数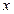 的范围是
的范围是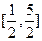 ⑶m=1,n=1
⑶m=1,n=1(1)对于函数 ,当
,当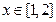 时,
时,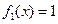 .
.
当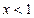 或
或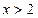 时,
时,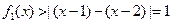 恒成立,故
恒成立,故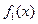 是“平底型”函数. (2分)
是“平底型”函数. (2分)
对于函数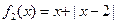 ,当
,当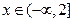 时,
时,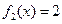 ;当
;当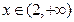 时,
时,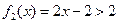 .
.
所以不存在闭区间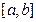 ,使当
,使当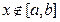 时,
时,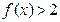 恒成立.
恒成立.
故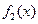 不是“平底型”函数. (4分)
不是“平底型”函数. (4分)
 (Ⅱ)若
(Ⅱ)若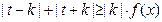 对一切
对一切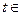 R恒成立,则
R恒成立,则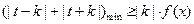 .
.
因为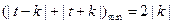 ,所以
,所以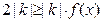 .又
.又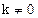 ,则
,则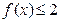 . (6分)
. (6分)
因为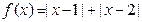 ,则
,则
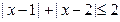 ,解得
,解得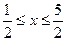 .
.
故实数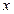 的范围是
的范围是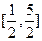 . (8分)
. (8分)
(Ⅲ)因为函数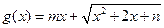 是区间
是区间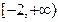 上的“平底型”函数,则存在区间
上的“平底型”函数,则存在区间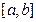
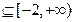 和常数
和常数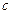 ,使得
,使得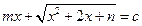 恒成立.
恒成立.
所以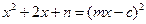 恒成立,即
恒成立,即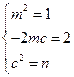 .解得
.解得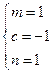 或
或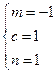 . (10分)
. (10分)
当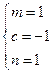 时,
时,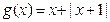 .
.
当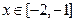 时,
时,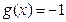 ,当
,当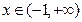 时,
时,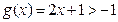 恒成立.
恒成立.
此时,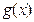 是区间
是区间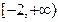 上的“平底型”函数. (11分)
上的“平底型”函数. (11分)
当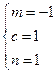 时,
时,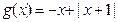 .
.
当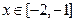 时,
时,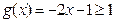 ,当
,当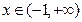 时,
时,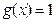 .
.
此时,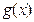 不是区间
不是区间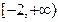 上的“平底型”函数. (13
上的“平底型”函数. (13 分)
分)
综上分析,m=1,n=1为所求. ……14分
 ,当
,当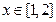 时,
时,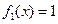 .
.当
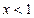 或
或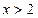 时,
时,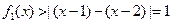 恒成立,故
恒成立,故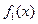 是“平底型”函数. (2分)
是“平底型”函数. (2分)对于函数
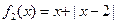 ,当
,当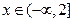 时,
时,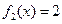 ;当
;当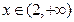 时,
时,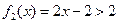 .
.所以不存在闭区间
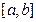 ,使当
,使当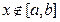 时,
时,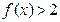 恒成立.
恒成立.故
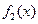 不是“平底型”函数. (4分)
不是“平底型”函数. (4分) (Ⅱ)若
(Ⅱ)若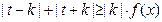 对一切
对一切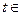 R恒成立,则
R恒成立,则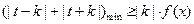 .
.因为
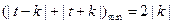 ,所以
,所以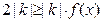 .又
.又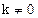 ,则
,则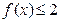 . (6分)
. (6分)因为
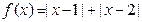 ,则
,则
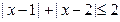 ,解得
,解得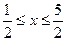 .
.故实数
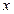 的范围是
的范围是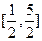 . (8分)
. (8分)(Ⅲ)因为函数
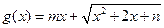 是区间
是区间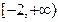 上的“平底型”函数,则存在区间
上的“平底型”函数,则存在区间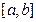
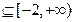 和常数
和常数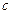 ,使得
,使得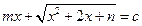 恒成立.
恒成立.所以
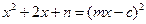 恒成立,即
恒成立,即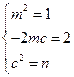 .解得
.解得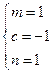 或
或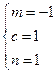 . (10分)
. (10分)当
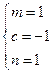 时,
时,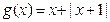 .
.当
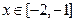 时,
时,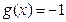 ,当
,当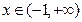 时,
时,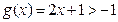 恒成立.
恒成立.此时,
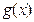 是区间
是区间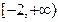 上的“平底型”函数. (11分)
上的“平底型”函数. (11分)当
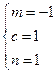 时,
时,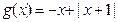 .
.当
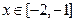 时,
时,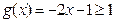 ,当
,当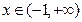 时,
时,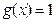 .
.此时,
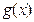 不是区间
不是区间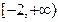 上的“平底型”函数. (13
上的“平底型”函数. (13 分)
分)综上分析,m=1,n=1为所求. ……14分

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
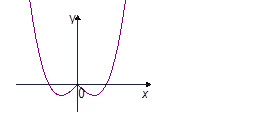
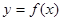 ,则图2中的图象对应的函数在下列四式中只可能是( )
,则图2中的图象对应的函数在下列四式中只可能是( )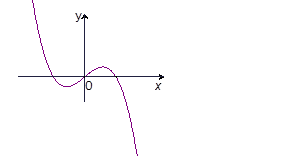
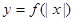
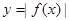
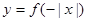
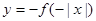
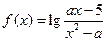 的定义域为
的定义域为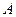 ,若命题
,若命题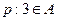 与命题
与命题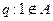 有且仅有一个为真命题,求实数
有且仅有一个为真命题,求实数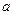 的取值范围。
的取值范围。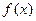 满足
满足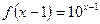 ,则函数
,则函数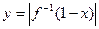 的图象是( )
的图象是( )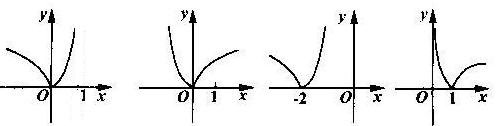
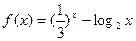 ,
,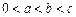 ,
,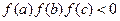 ,实数
,实数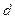 是函数
是函数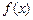 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断: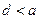 ;②
;②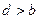 ;③
;③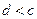 ;④
;④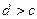 .
.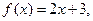 则函数
则函数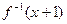 的反函数是
的反函数是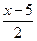
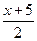
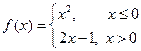 ,若
,若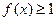 ,则
,则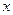 的取值范围是( )
的取值范围是( )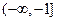 B.
B.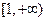 C.
C.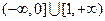 D.
D.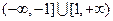
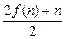 (n∈N*)且f(1)=2,则f(20)为( )
(n∈N*)且f(1)=2,则f(20)为( )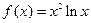 的单调递减区间为 .
的单调递减区间为 .