题目内容
11.函数y=tan$\frac{πx}{4}$,x∈(2,6)的图象与x轴交于A点,过点A的直线l与函数的图象交于B,C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$=( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
分析 根据题意,求出A点的坐标,设出B,C两点的坐标,根据B、C与A三点的关系,求出向量的数量积即可.
解答 解:y=tan$\frac{π}{4}$x,x∈(2,6),
∴$\frac{π}{4}$x∈($\frac{π}{2}$,$\frac{3π}{2}$);
∵y的图象与x轴交于A点,
∴$\frac{π}{4}$x=π,解得x=4;
∴A(4,0);
∵过点A的直线l与函数的图象交于B,C两点,
设B(x1,y1),C(x2,y2),
∵过点A的直线l与函数的图象交于B、C两点,
∴B,C 两点关于A对称,
即x1+x2=8,y1+y2=0;如图所示,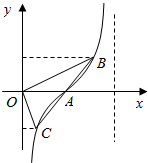
又$\overrightarrow{OA}$=(4,0),
$\overrightarrow{OB}$+$\overrightarrow{OC}$=(x1+x2,y1+y2),
∴($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$=4×(x1+x2)+0×(y1+y2)=4×8=32.
故选:D.
点评 本题考查了正切函数的图象与性质的应用问题,也考查了平面向量的坐标运算与数量积的应用问题,是综合性题目.

练习册系列答案
相关题目
6.某校有学生1000人,其中高一学生400人.为调查学生了解消防知识的现状,采用按年级分层抽样的方法,从该校学生中抽取一个40人的样本,那么样本中高一学生的人数为( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
