题目内容

17．设变量x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥x}\\{3x+2y≤15}\end{array}\right.$，则z=log2（2x+y）的最大值为log29．

分析 画出满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥x}\\{3x+2y≤15}\end{array}\right.$的可行域，先求出真数的最大值，进而可得答案．

解答 解：满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥x}\\{3x+2y≤15}\end{array}\right.$的可行域如下图所示：

令U=2x+y，则UA=3，UB=9，UC=8，
故当x=y=3时，2x+y取最大值9，
此时z=log2（2x+y）的最大值为log29，
故答案为：log29

点评 本题考查的知识点是线性规划，对数函数的单调性，是对数函数与线性规划的综合考查，难度中档．

练习册系列答案
相关题目
7．若sinx=-1，x∈[0，2π]，则x为$\frac{3π}{2}$．
8．已知函数f（x）=loga（1-x）+loga（x+3），其中0＜a＜1，记函数f（x）的定义域为D．
（1）求函数f（x）的定义域D；
（2）求函数f（x）的值域．
5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点为F（2，0），且过点（0，$\sqrt{2}$）．
（1）求此椭圆的方程；
（2）是否存在过点F且斜率为k的直线l与椭圆C交于A，B两点，使得∠AOB为锐角？若存在，求实数k的取值范围；若不存在，请说明理由．
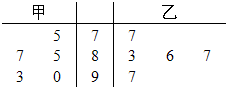12．甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示．
（1）分别在甲乙的5次成绩中任取一次，至少有一个成绩高于80的概率；
（2）若将频率视为概率，对学生甲和乙在今后的两次英语口语竞赛成绩进行预测，记两人成绩都高于85分的次数为ξ，求ξ的分布列及数学期望Eξ．
2．已知数列{an}的前n项和为Sn，a1=-1，an+1=SnSn+1（n∈N*）．则an=$\left\{\begin{array}{l}{-1，n=1}\\{\frac{1}{n（n-1）}，n≥2}\end{array}\right.$．
9．求值：（1）$\root{6}{24}$×$\root{3}{3}$×$\sqrt{\frac{3}{2}}$；
（2）已知lg2=a，lg3=b，求lg$\frac{9}{5}$．（用a，b表示）
6．若a，b为实数，且（5a+6）2+（b-3）2=0，求$\frac{a}{b}$的值．
11．函数y=tan$\frac{πx}{4}$，x∈（2，6）的图象与x轴交于A点，过点A的直线l与函数的图象交于B，C两点，则（$\overrightarrow{OB}$+$\overrightarrow{OC}$）•$\overrightarrow{OA}$=（　　）
A．4B．8C．16D．32

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网