题目内容

定义f（M）=（m，n，p），其中M是△ABC内一点，m、n、p分别是△MBC、△MCA、△MAB的面积，已知△ABC中，
AB
•
AC
=2
3
，∠BAC=30°，f(N)=(
1
2
，x，y)，则
1
x
+
4
y
的最小值是（　　）
A．8B．9C．16D．18
∵
AB
•
AC
=2
3
，∠BAC=30°，
所以由向量的数量积公式得 |
AB
|•|
AC
|•cos∠BAC=2
3
，
∴|
AB
||
AC
|=4，
∵S△ABC=
1
2
|
AB
|•|
AC
|•sin∠BAC=1，
由题意得，
x+y=1-
1
2
=
1
2
．
1
x
+
4
y
=2(
1
x
+
4
y
)(x+y)=2（5+
y
x
+
4x
y
≥2(5+2
y
x
•
4x
y
)=18，等号在x=
1
6
，y=
1
3
取到，所以最小值为18．
故选D．
练习册系列答案
相关题目
若直线ax+2by-2=0（a，b∈（0，+∞））平分圆x2+y2-4x-2y-6=0，则
1
a
+
2
b
的最小值是______．
已知正数x、y满足xy=x+y+3．
（1）求xy的范围；
（2）求x+y的范围．
已知函数y=x+
16
x+2
，x∈(-2，+∞)，则此函数的最小值为______．
下列四个结论中，正确结论为（　　）
A．当x＞0且x≠1时，lgx+
1
lgx
≥2
B．当x＞0时，
x
+
1
x
≥2
C．当x≥0时，x+
1
x
的最小值为2
D．当x＞0时，x3+
1
x
的最小值为2
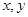x、y满足约束条件
x+y≥1
x-y≥-1
2x-y≤2
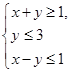，若目标函数z=ax+by（a＞0，b＞0）的最大值为7，则
3
a
+
4
b
的最小值为（　　）
A．14B．7C．18D．13
已知0＜x＜
1
2
，则y=
1
2
x(1-2x)取最大值时x的值是（　　）
A．
1
3
B．
1
4
C．
1
2
D．
2
3
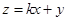已知变量满足约束条件，若的最大值为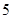，则实数      ．
若的最大值是3，则的值是              .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网