题目内容
10.设M、N为△ABC内一点,且→AM=34→AB+45→AC,→AN=34→AB+67→AC,则S△ABMS△ABN=1415.分析 先根据题意画出图形,然后根据△ABM与△ABN的面积之比等于高之比,转化成AP与AQ之比,从而求出所求.
解答 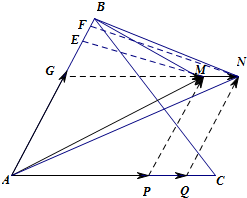 解:根据平面向量的基本定理作出对应的图象如图:
解:根据平面向量的基本定理作出对应的图象如图:
则A,M,N三点共线,且AP=45AC,AQ=67AC
故△ABM,△ABN面积之比等于高之比,
设EM,FN分别是△ABM,△ABN的高,
则根据三角形相似的性质可知EMFN=GMGN=APAQ=45AC67AC=1415,
则S△ABMS△ABN=12AB•EM12AB•FN=EMFN=1415,
故答案为:1415,
点评 本题主要考查了向量在几何中的应用,解题的关键就是画出图形,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知ω>0,0<φ<π,点A(\frac{π}{4},0)和点B(\frac{5π}{4},0)是函数f(x)=sin(ωx+φ)的图象的两个相邻的对称中心,则φ=( )
| A. | \frac{π}{4} | B. | \frac{π}{3} | C. | \frac{π}{2} | D. | \frac{3π}{4} |

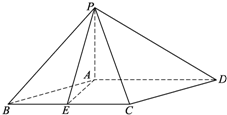 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.