题目内容

1．数列{an}中，an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$，a1=2，则数列{an}的前2015项的积等于3．

分析 通过计算出数列前几项的值，判断该数列为周期数列，进而可得结论．

解答 解：∵${a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}$且a1=2，
∴a2=$\frac{1+{a}_{1}}{1-{a}_{1}}$=$\frac{1+2}{1-2}$=-3，
a3=$\frac{1+{a}_{2}}{1-{a}_{2}}$=$\frac{1-3}{1+3}$=-$\frac{1}{2}$，
a4=$\frac{1+{a}_{3}}{1-{a}_{3}}$=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$，
a5=$\frac{1+{a}_{4}}{1-{a}_{4}}$=$\frac{1+\frac{1}{3}}{1-\frac{1}{3}}$=2，
不难发现数列{an}是周期数列，
四个为一周期且最前四个乘积为$2×（-3）×（-\frac{1}{2}）×\frac{1}{3}$=1，
∵2015=503×4+3，
∴数列{an}前2015项的积为：${1}^{503}×2×（-3）×（-\frac{1}{2}）$=3，
故答案为：3．

点评 本题考查求数列的前n项的乘积，找出其周期是解决本题的关键，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
11．已知圆心为C（-2，6）的圆经过点M（0，6-2$\sqrt{3}$）
（1）求圆C的标准方程；
（2）若直线l过点P（0，5）且被圆C截得的线段长为4$\sqrt{3}$，求直线l的方程．
12．设λ∈R，f（x）=$\overrightarrow a•\overrightarrow b$，其中$\overrightarrow a=（{cosx，sinx}），\overrightarrow b=（{λsinx-cosx，cos（\frac{π}{2}-x）}）$，已知f（x）满足$f（{-\frac{π}{3}}）=f（0）$
（1）求函数f（x）的单调递增区间；
（2）求不等式$2cos（2x-\frac{π}{6}）＞\sqrt{3}$的解集．
9．已知递增的等比数列{an}前三项之积为8，且这三项分别加上1、2、2后又成等差数列．
（1）求等比数列{an}的通项公式；
（2）记bn=an+2n，求数列{bn}的前n项和Tn．
16．函数f（x）=x2，（x＜-2）的反函数是$y=-\sqrt{x}，（x＞4）$．
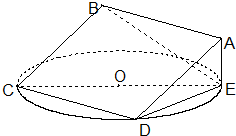6．如图，正方形ABCD所在平面与圆O所在平面相交于CD，CE为圆O的直径，线段CD为圆O的弦，AE垂直于圆O所在平面．
（1）求证：CD⊥平面AED；
（2）设异面直线CB与DE所成的角为$\frac{π}{6}$且AE=1，将△ACD（及其内部）绕AE所在直线旋转一周形成一几何体，求该几何体的体积．
13．设函数f（x）对任意x∈R，都有f（2x）=a•f（x），其中a为常数．当x∈[1，2）时，$f（x）=sin（\frac{π}{2}x）$．
（1）设a＞0，f（x）在x∈[4，8）时的解析式及其值域；
（2）设-1≤a＜0，求f（x）在x∈[1，+∞）时的值域．
10．设M、N为△ABC内一点，且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AC}$，$\overrightarrow{AN}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{6}{7}$$\overrightarrow{AC}$，则$\frac{{S}_{△ABM}}{{S}_{△ABN}}$=$\frac{14}{15}$．
11．设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，其中向量$\overrightarrow{a}$=（m，cos2x），$\overrightarrow{b}$=（1+sin2x，1），x∈R，且y=f（x）的图象经过点（$\frac{π}{4}$，2）
（1）求实数m的值；
（2）求函数y=f（x）的最小正周期；
（3）求函数y=f（x）的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网