题目内容
15.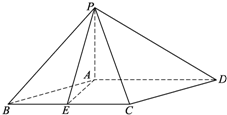 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.(1)求证:PE⊥AD;
(2)求平面PAE与平面PCD所成锐二面角的余弦值;
(3)在线段PD上是否存在一点F,使得CF∥平面PAE,并给出证明.
分析 (1)建立空间坐标系,利用向量法即可证明PE⊥AD;
(2)求出平面的法向量,利用向量法即可求平面PAE与平面PCD所成锐二面角的余弦值;
(3)根据线面平行的判定定理,结合向量法进行求解即可.
解答 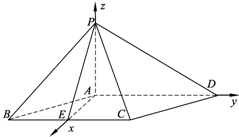 解:∵四边形ABCD是∠ABC=60°的菱形,E为边BC的中点,
解:∵四边形ABCD是∠ABC=60°的菱形,E为边BC的中点,
∴AE⊥BC,∴AE⊥AD,又PA⊥平面ABCD,
∴PA⊥AE,PA⊥AD,以AE、AD、AP分别为x、y、z轴建立坐标系如图,设AB=2,
则B($\sqrt{3}$,-1,0),E($\sqrt{3}$,0,0),C($\sqrt{3}$,1,0),D(0,2,0),P(0,0,1)….(1分)
(1)$\overrightarrow{PE}$=($\sqrt{3}$,0,-1),$\overrightarrow{AD}$=(0,2,0)…(2分)
$\overrightarrow{PE}$•$\overrightarrow{AD}$=0…(3分)
∴PE⊥AD…(4分)
(2)设平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{n}$⊥$\overrightarrow{PC}$,$\overrightarrow{n}$⊥$\overrightarrow{PD}$,
∵$\overrightarrow{PC}$=($\sqrt{3}$,1,-1),$\overrightarrow{PD}$=(0,2,-1),
∴(x,y,z)•($\sqrt{3}$,1,-1)=$\sqrt{3}$x+y-z=0,(x,y,z)•(0,2,-1)=2y-z=0,
令x=1,则y=$\sqrt{3}$,z=2$\sqrt{3}$,得平面PCD的一个法向量为$\overrightarrow{n}$=(1,$\sqrt{3}$,2$\sqrt{3}$),
又AD⊥平面PAE,则$\overrightarrow{AD}$=(0,2,0)是面PAE的一个法向量,
设平面PAE与平面PCD所成角为α,
则cosα=|cos<$\overrightarrow{n}$,$\overrightarrow{AD}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{AD}}{|\overrightarrow{n}|•|\overrightarrow{AD}|}$|=$\frac{2\sqrt{3}}{\sqrt{16}×2}$=$\frac{\sqrt{3}}{4}$…(8分)
(3)假设线段PD存在一点F,使直线CF∥平面PAE,则CF⊥面PAD,
∴CF⊥AD,
设$\overrightarrow{PF}$=λ$\overrightarrow{PD}$=(0,2λ,-λ),(0≤λ≤1),则$\overrightarrow{CF}$=$\overrightarrow{PF}$-$\overrightarrow{PC}$=(-$\sqrt{3}$,2λ-1,-λ+1),
则$\overrightarrow{CF}•\overrightarrow{AD}$=(-$\sqrt{3}$,2λ-1,-λ+1)•(0,2,0)=4λ-2=0,
解得,λ=$\frac{1}{2}$,
∴当F为线段PD的中点时,直线CF∥平面PAE…(12分)
点评 本题主要考查空间直线垂直,线面平行的判定以及二面角的求解,建立坐标系,利用向量法是解决本题的关键.

| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | 2 |
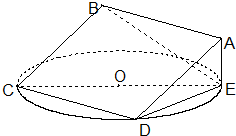 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.