题目内容
已知抛物线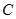 :
: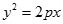 的焦点为圆
的焦点为圆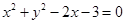 的圆心,直线
的圆心,直线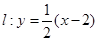 与
与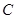 交于不同的两点
交于不同的两点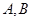 .
.
(1) 求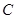 的方程;
的方程;
(2) 求弦长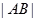 。
。
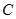 :
: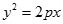 的焦点为圆
的焦点为圆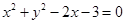 的圆心,直线
的圆心,直线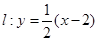 与
与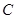 交于不同的两点
交于不同的两点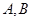 .
.(1) 求
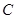 的方程;
的方程;(2) 求弦长
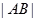 。
。 (1)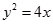 。(2)
。(2)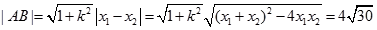 。
。
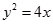 。(2)
。(2)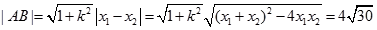 。
。试题分析:(1)由于圆的方程
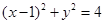 ,可知圆心为
,可知圆心为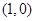 ,故有
,故有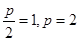 ,得到抛物线方程。
,得到抛物线方程。(2)联立抛物线于直线的方程,借助于韦达定理得到弦长
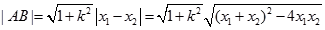 的值。
的值。解:(1)
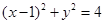 ,圆心
,圆心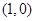 ,
,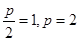 ,所以
,所以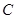 的方程为
的方程为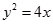 。
。(2)
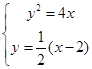 ,消去
,消去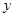 ,
,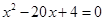 ,
,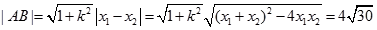 。
。点评:解决该试题的关键是通过圆心坐标得到P的值,进而得到抛物线方程,然后借助于联立方程组得到相交弦的长度的表示。

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
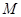 过两点
过两点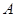 (1,-1),
(1,-1),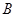 (-1,1),且圆心
(-1,1),且圆心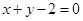 上.
上.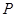 是直线
是直线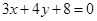 上的动点,
上的动点,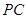 、
、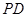 是圆
是圆 、
、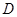 为切点,求四边形
为切点,求四边形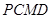 面积的最小值.
面积的最小值.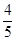 |PD|.
|PD|.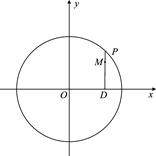
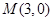 是圆
是圆 :
: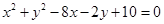 内一点,过
内一点,过 被圆截得的弦最短的直线方程是( )
被圆截得的弦最短的直线方程是( )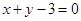
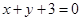

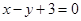
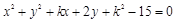 相切,则实数
相切,则实数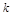 的取值范围是( )
的取值范围是( )
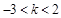
 或
或
 或
或
 上,与直线
上,与直线 相切,在
相切,在 上截得弦长为6,求该圆的方程.
上截得弦长为6,求该圆的方程.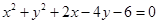 表示的图形是( )
表示的图形是( ) 为圆心,
为圆心, 为半径的圆
为半径的圆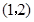 为圆心,
为圆心,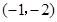 为圆心,
为圆心,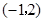 为圆心,
为圆心,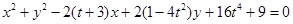 表示一个圆.
表示一个圆. 的取值范围
的取值范围