题目内容
2.已知函数f(x)=$\frac{a}{3}$x3-ax2+x+1在x=x1和x=x2处有极值,且1<$\frac{{x}_{1}}{{x}_{2}}$≤5.(1)求a的取值范围;
(2)当a取最大值时,存在t∈R,使得x∈[1,m](m>1),f′(t-x)≤$\frac{36}{5}$x-$\frac{4}{5}$恒成立,求m的最大值.
分析 (1)通过韦达定理得到x1+x2,x1x2,结合$\frac{{x}_{2}}{{x}_{1}}$的范围,得到$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的范围,从而求出的范围;
(2)令u=t-x,u∈[t-m,t-1],得到y=-$\frac{9}{5}$(u-1)2+1,通过讨论t的范围得到不等式,求出m的最大值即可.
解答 解:(1)令f′(x)=ax2-2ax+1=0
∴x1+x2=2,x1x2=$\frac{1}{a}$,
∵1<$\frac{{x}_{1}}{{x}_{2}}$≤5,∴$\frac{1}{5}$≤$\frac{{x}_{2}}{{x}_{1}}$<1,
$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$∈($\frac{6}{5}$,6),
$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{{(x}_{1}{+x}_{2})}^{2}-{{2x}_{1}x}_{2}}{{{x}_{1}x}_{2}}$=$\frac{4-\frac{2}{a}}{\frac{1}{a}}$∈($\frac{6}{5}$,6)
解得:a∈($\frac{4}{5}$,2)
(2):[f(t-x)]′=-f′(t-x)=-a(t-x)2+2a(t-x)-1,
令u=t-x,u∈[t-m,t-1],
∴y=-$\frac{9}{5}$(u-1)2+1,
①当t-1≤1即t≤2时:
ymax=yt-1=-$\frac{9}{5}$(t-2)2+$\frac{4}{5}$≤$\frac{36}{5}$m-$\frac{4}{5}$,
解得:m≤$\frac{9}{2}$,
②当2<t<m+1时:ymax=$\frac{4}{5}$≤$\frac{36}{5}$m-$\frac{4}{5}$,
解得:m≤$\frac{9}{2}$,
③当t≥m+1时:ymax=-$\frac{9}{5}$(t-m+1)2+$\frac{4}{5}$≤$\frac{4}{5}$,
综上:m≤$\frac{9}{2}$.
故m的最大值是;$\frac{9}{2}$.
点评 本题考查了导数的应用,函数的单调性问题,考查分类讨论,是一道中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (2,+∞) | B. | (-∞,-3) | C. | ($\sqrt{2}$,2) | D. | (-8,-4) |
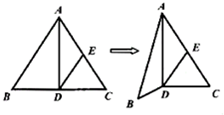 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |