题目内容
(本题满分12分)
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为.点P(1,)、A、B在椭圆E上,且+=m(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为.点P(1,)、A、B在椭圆E上,且+=m(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
(1)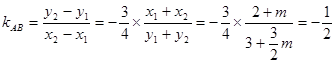 ;
;
(2)x+2y+2=0.
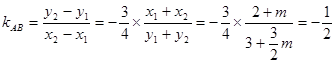 ;
;(2)x+2y+2=0.
本试题主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的运用。
(1)由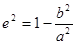 =
= 及
及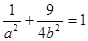 解得a2=4,b2=3,
解得a2=4,b2=3,
椭圆方程为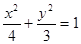 ;再设出点A,B,利用点差法得到斜率。
;再设出点A,B,利用点差法得到斜率。
(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足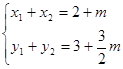
点P的坐标为(1,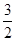 ), m=-3, 于是x1+x2+1=3+m=0,y1+y2+
), m=-3, 于是x1+x2+1=3+m=0,y1+y2+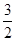 =3+
=3+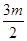 +
+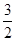 =0,
=0,
因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
,进而得到直线的方程。
解:(1)由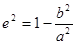 =
= 及
及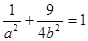 解得a2=4,b2=3,
解得a2=4,b2=3,
椭圆方程为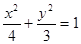 ;
;
设A(x1,y1)、B(x2,y2),由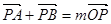 得
得
(x1+x2-2,y1+y2-3)=m(1,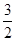 ),即
),即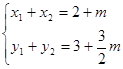
又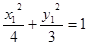 ,
, ,两式相减得
,两式相减得
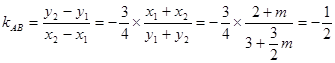 ;
;
(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足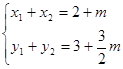 ,
,
点P的坐标为(1,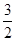 ), m=-3, 于是x1+x2+1=3+m=0,y1+y2+
), m=-3, 于是x1+x2+1=3+m=0,y1+y2+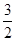 =3+
=3+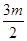 +
+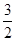 =0,
=0,
因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
∵x1+x2=-1,y1+y2=-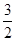 ,∴AB中点坐标为(
,∴AB中点坐标为(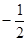 ,
,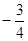 ),
),
又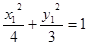 ,
, ,两式相减得
,两式相减得
 ;
;
∴直线AB的方程为y+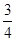 =
=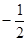 (x+
(x+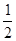 ),即x+2y+2=0.
),即x+2y+2=0.
(1)由
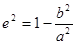 =
= 及
及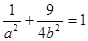 解得a2=4,b2=3,
解得a2=4,b2=3,椭圆方程为
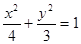 ;再设出点A,B,利用点差法得到斜率。
;再设出点A,B,利用点差法得到斜率。(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足
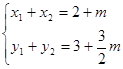
点P的坐标为(1,
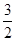 ), m=-3, 于是x1+x2+1=3+m=0,y1+y2+
), m=-3, 于是x1+x2+1=3+m=0,y1+y2+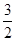 =3+
=3+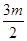 +
+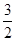 =0,
=0,因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
,进而得到直线的方程。
解:(1)由
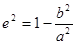 =
= 及
及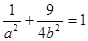 解得a2=4,b2=3,
解得a2=4,b2=3,椭圆方程为
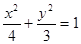 ;
;设A(x1,y1)、B(x2,y2),由
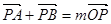 得
得(x1+x2-2,y1+y2-3)=m(1,
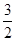 ),即
),即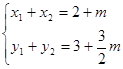
又
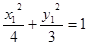 ,
, ,两式相减得
,两式相减得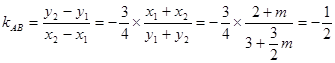 ;
;(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足
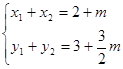 ,
,点P的坐标为(1,
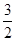 ), m=-3, 于是x1+x2+1=3+m=0,y1+y2+
), m=-3, 于是x1+x2+1=3+m=0,y1+y2+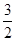 =3+
=3+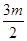 +
+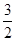 =0,
=0,因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
∵x1+x2=-1,y1+y2=-
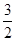 ,∴AB中点坐标为(
,∴AB中点坐标为(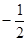 ,
,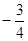 ),
),又
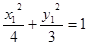 ,
, ,两式相减得
,两式相减得 ;
;∴直线AB的方程为y+
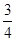 =
=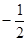 (x+
(x+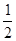 ),即x+2y+2=0.
),即x+2y+2=0.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :
: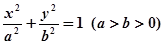 的中心
的中心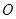 为圆心,
为圆心, 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆 ,左焦点为
,左焦点为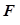 ,上顶点为
,上顶点为 ,且满足
,且满足 ,
,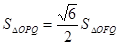 .
. 及其“准圆”的方程;
及其“准圆”的方程; (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆 、
、 两点,试证明:当
两点,试证明:当 时,试问弦
时,试问弦 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点, 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )

 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________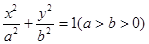 上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2
上有一动点P,P到椭圆C的两焦点 F1,F2的距离之和等于2 ,△PF1F2的面积最大值为1
,△PF1F2的面积最大值为1 (O为坐标原点)且
(O为坐标原点)且 | ,求实数t的取值范围.
| ,求实数t的取值范围. 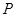 是椭圆
是椭圆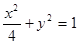 上的在第一象限内的点,又
上的在第一象限内的点,又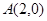 、
、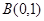 ,
,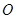 是原点,则四边形
是原点,则四边形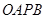 的面积的最大值是 。
的面积的最大值是 。 轴上的双曲线的离心率
轴上的双曲线的离心率 ,其焦点到渐近线的距离为1,则此双曲线的方程为( )
,其焦点到渐近线的距离为1,则此双曲线的方程为( )



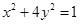 的离心率为( )
的离心率为( )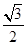
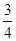
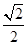
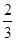
 的焦点为
的焦点为 和
和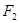 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么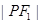 是
是 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍