题目内容
已知中心在原点,焦点在 轴上的双曲线的离心率
轴上的双曲线的离心率 ,其焦点到渐近线的距离为1,则此双曲线的方程为( )
,其焦点到渐近线的距离为1,则此双曲线的方程为( )
 轴上的双曲线的离心率
轴上的双曲线的离心率 ,其焦点到渐近线的距离为1,则此双曲线的方程为( )
,其焦点到渐近线的距离为1,则此双曲线的方程为( )A. | B. |
C. | D. |
D
设双曲线的方程为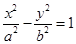 ,∵
,∵
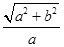 即
即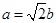 ,又焦点到渐近线的距离为b=1,∴
,又焦点到渐近线的距离为b=1,∴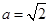 ,∴双曲线的方程为
,∴双曲线的方程为 ,故选D
,故选D
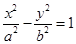 ,∵
,∵
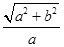 即
即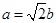 ,又焦点到渐近线的距离为b=1,∴
,又焦点到渐近线的距离为b=1,∴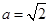 ,∴双曲线的方程为
,∴双曲线的方程为 ,故选D
,故选D
练习册系列答案
相关题目
题目内容
 轴上的双曲线的离心率
轴上的双曲线的离心率 ,其焦点到渐近线的距离为1,则此双曲线的方程为( )
,其焦点到渐近线的距离为1,则此双曲线的方程为( )A. | B. |
C. | D. |
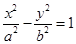 ,∵
,∵
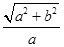 即
即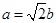 ,又焦点到渐近线的距离为b=1,∴
,又焦点到渐近线的距离为b=1,∴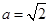 ,∴双曲线的方程为
,∴双曲线的方程为 ,故选D
,故选D