题目内容
1．已知集合A={x|$\frac{x-1}{x+2}$≥0}，B={x|x≤a}，若A∩B=B，则a的取值范围是（ ）| A． | a≥1 | B． | a≥2 | C． | a≤-2 | D． | a＜-2 |
分析 求出A中不等式的解集确定出A，根据A与B的交集为B，得到B为A的子集，确定出a的范围即可．
解答 解：由A中不等式变形得：（x-1）（x+2）≥0，且x+2≠0，
解得：x＜-2或x≥1，即A={x|x＜-2或x≥1}，
∵A∩B=B，B={x|x≤a}，
∴B⊆A，
则a的范围为a＜-2，
故选：D．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
12．某商场为了了解顾客的购物信息，随机的在商场收集了100位顾客购物的相关数据，整理如下：
统计结果显示100位顾客中购物款不低于100元的顾客共60位，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．
（Ⅰ）试确定m，n的值，并据上述数据估计该商场每日应准备纪念品的数量；
（Ⅱ）若商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款 小于200元的按购物款的百分比返利，具体见下表：
若用各组购物款的中位数估计该组的购物款，请据上述数据估计该商场日均让利多少元？
| 一次购物款（单位：元） | [0，50） | [50，100） | [100，150） | [150，200） | [200，+∞） |
| 顾客人数 | m | 20 | 30 | n | 10 |
（Ⅰ）试确定m，n的值，并据上述数据估计该商场每日应准备纪念品的数量；
（Ⅱ）若商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物款 小于200元的按购物款的百分比返利，具体见下表：
| 一次购物款（单位：元） | [0，50） | [50，100） | [100，150） | [150，200） |
| 返利百分比 | 0 | 6% | 8% | 10% |
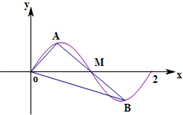如图，过点M（1，0）的直线与函数y=sinπx（0≤x≤2）的图象交于A，B两点，则$\overrightarrow{OM}$•（$\overrightarrow{OA}$+$\overrightarrow{OB}$）等于（ ）
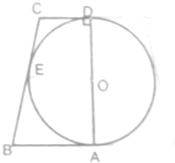如图，半圆O的直径为直角梯形垂直于底的腰，且切AB、BC、CD于A、E、D点，将其绕AD所在直线旋转一周，得到一个球与一个圆台，若球的表面积与圆台侧面积的比为3：4，求球的体积与圆台体积之比．