题目内容
19.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am、an,使得aman=16a12,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )| A. | $\frac{3}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{11}{4}$ | D. | 不存在 |
分析 设{an}的公比为q(q>0),由等比数列的通项公式化简a7=a6+2a5,求出q,代入aman=16a12化简得m,n的关系式,由“1”的代换和基本不等式求出式子的范围,验证等号成立的条件,由m、n的值求出式子的最小值.
解答 解:设正项等比数列{an}的公比为q,且q>0,
由a7=a6+2a5得:a6q=a6+$\frac{2{a}_{6}}{q}$,
化简得,q2-q-2=0,解得q=2或q=-1(舍去),
因为aman=16a12,所以$({a}_{1}{q}^{m-1})$$({a}_{1}{q}^{n-1})$=16a12,
则qm+n-2=16,解得m+n=6,
所以$\frac{1}{m}+\frac{9}{n}$=$\frac{1}{6}$(m+n)($\frac{1}{m}+\frac{9}{n}$)=$\frac{1}{6}$(10+$\frac{n}{m}+\frac{9m}{n}$)≥$\frac{1}{6}(10+2\sqrt{\frac{n}{m}•\frac{9m}{n}})$=$\frac{8}{3}$,
当且仅当$\frac{n}{m}=\frac{9m}{n}$时取等号,此时$\left\{\begin{array}{l}{\frac{n}{m}=\frac{9m}{n}}\\{m+n=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=\frac{9}{2}}\end{array}\right.$,
因为m n取整数,所以均值不等式等号条件取不到,则$\frac{1}{m}+\frac{9}{n}$>$\frac{8}{3}$,
验证可得,当m=2、n=4时,$\frac{1}{m}+\frac{9}{n}$取最小值为$\frac{11}{4}$,
故选:C.
点评 本题考查等比数列的通项公式,利用“1”的代换和基本不等式求最值问题,考查化简、计算能力,注意等号的成立的条件,属于易错题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
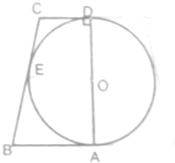 如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比.
如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比.