题目内容
设奇函数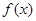 在
在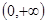 上是增函数,且
上是增函数,且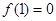 ,则不等式
,则不等式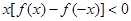 的解集为( )
的解集为( )
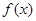 在
在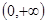 上是增函数,且
上是增函数,且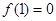 ,则不等式
,则不等式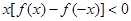 的解集为( )
的解集为( )A.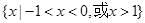 | B. |
C.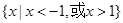 | D.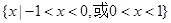 |
D
本试题主要是考查了抽象函数的单调性、奇偶性和不等式的求解问题。
∵函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,
∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),
∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,
即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.
综上,不等式x[f(x)-f(-x)]<0的解集为{x|-1<x<0,或0<x<1},故选D.
解决该试题的关键是将所求的不等式结合奇函数化简为xf(x)<0,然后分类讨论得到结论。
∵函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,
∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),
∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,
即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.
综上,不等式x[f(x)-f(-x)]<0的解集为{x|-1<x<0,或0<x<1},故选D.
解决该试题的关键是将所求的不等式结合奇函数化简为xf(x)<0,然后分类讨论得到结论。

练习册系列答案
相关题目
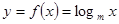 ,
,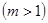 在
在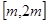 上的最大值是最小值的2倍,
上的最大值是最小值的2倍,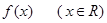 的图象如图所示,则函数
的图象如图所示,则函数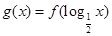 的单调减区间是____.
的单调减区间是____.
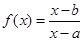 在区间
在区间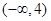 上是增函数,则有( )
上是增函数,则有( )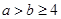
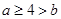
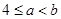
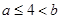
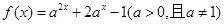
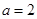 ,求
,求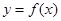 的值域
的值域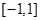 上有最大值14。求
上有最大值14。求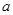 的值;
的值; 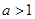 ,作出
,作出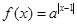 的草图,并通过图象求出函数
的草图,并通过图象求出函数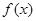 的单调区间
的单调区间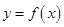 是定义在R上的减函数,且
是定义在R上的减函数,且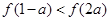 ,
,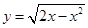 的单调递减区间是 __________________.
的单调递减区间是 __________________.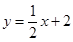 ,则
,则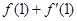 = .
= .