题目内容
【题目】已知函数![]() 在点
在点![]() 处的切线与y轴垂直.
处的切线与y轴垂直.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() 成立,求a的取值范围
成立,求a的取值范围
【答案】(1)见解析;(2)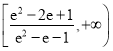
【解析】
(1)令f′(1)=0求出b,再根据f′(x)的符号得出f(x)的单调区间;
(2)分类讨论,分别求出![]() 在(0,e)上的最小值,即可得出a的范围.
在(0,e)上的最小值,即可得出a的范围.
(1)![]() ,由题
,由题![]() ,
,
解得![]() ,由
,由![]() ,得
,得![]() .
.
因为![]() 的定义域为
的定义域为![]() ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() ,
, ![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
(2)由(1)知![]() ,
,
所以![]()
(ⅰ)若![]() ,则由(1)知
,则由(1)知![]() ,即
,即![]() 恒成立
恒成立
(ⅱ)若![]() ,则
,则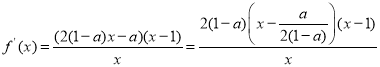 且
且![]()
故当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
![]() ,即
,即![]() 恒成立
恒成立
(ⅲ)若![]() ,则
,则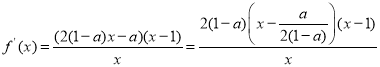 且
且![]()
故当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
由题只需![]() 即可,即
即可,即![]() ,解得
,解得![]() ,
,
而由![]() ,且
,且![]() ,
,
得![]()
(ⅳ)若![]() ,则
,则![]() ,
,![]() 为增函数,且
为增函数,且![]() ,
,
所以![]() ,
,![]() ,不合题意,舍去;
,不合题意,舍去;
(ⅴ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 上都为增函数,且
上都为增函数,且![]()
所以![]() ,
,![]() ,不合题意,舍去;
,不合题意,舍去;
综上所述,a的取值范围是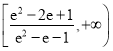

【题目】某公司的营销部门对某件商品在网上销售情况进行调查,发现当这件商品每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到以下表:
![]()
(1)经分析发现,可用线性回归模型拟合该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)该公司为了在购物节期间对所有商品价格进行新一轮调整,随机抽查了上一年购物节期间60名网友的网购金额情况,得到如下数据统计表:
网购金额 (单位:千元) |
|
|
|
|
|
| 合计 |
频数 | 3 | 9 | 9 | 15 | 18 | 6 | 60 |
若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”.该营销部门为了进步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设![]() 为选取的3人中“网购达人”的人数,求
为选取的3人中“网购达人”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:①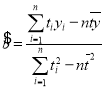 ,
,![]() ;②
;②![]() .
.