题目内容
【题目】设椭圆![]() ,其长轴长是短轴长的
,其长轴长是短轴长的![]() 倍,过焦点且垂直于
倍,过焦点且垂直于![]() 轴的直线被椭圆截得的弦长为
轴的直线被椭圆截得的弦长为![]() .
.
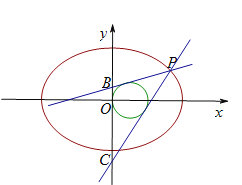
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 是椭圆
是椭圆![]() 上横坐标大于
上横坐标大于![]() 的动点,点
的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]() ,试判断点
,试判断点![]() 在何位置时
在何位置时![]() 的长度最小,并证明你的判断.
的长度最小,并证明你的判断.
【答案】(1)![]() ;(2)点
;(2)点![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度最小.见解析.
的长度最小.见解析.
【解析】
(1)根据条件列方程组,解得![]() ;
;
(2)先设![]() ,
,![]() ,根据点斜式得直线
,根据点斜式得直线![]() 的方程,再根据直线与圆相切列等量关系得
的方程,再根据直线与圆相切列等量关系得![]() ,类似可得
,类似可得![]() ,转化为
,转化为![]() 是方程
是方程![]() 的两个根,利用韦达定理解得
的两个根,利用韦达定理解得![]() ,根据
,根据![]() 点满足椭圆方程,代入化简得
点满足椭圆方程,代入化简得![]() ,最后根据
,最后根据![]() 范围以及函数单调性求最值,即得结果.
范围以及函数单调性求最值,即得结果.
(1)由已知![]() ,
,
因为过焦点且垂直于![]() 轴的直线被椭圆截得的弦长为
轴的直线被椭圆截得的弦长为![]() ,
,![]() ,
,
解得![]() ,故所求椭圆方程为
,故所求椭圆方程为![]() .
.
(2)设![]() ,
,![]() .
.
不妨设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即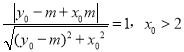 ,
,
化简得![]() 同理,
同理,![]() ,
,
![]() 是方程
是方程![]() 的两个根,
的两个根,
![]() ,则
,则![]() ,
,
![]() 是椭圆上的点,∴
是椭圆上的点,∴![]() ,
,![]() .
.
令![]() ,令
,令![]() ,则
,则![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 取到最小值,此时
取到最小值,此时![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度最小.
的长度最小.

练习册系列答案
相关题目