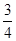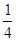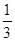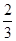题目内容
(本小题满分13分)
已知椭圆
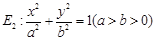 .
.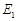 与
与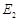 有相同的离心率,过点
有相同的离心率,过点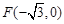 的直线
的直线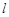 与
与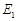 ,
,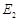 依次交于A,C,D,B四点(如图).当直线
依次交于A,C,D,B四点(如图).当直线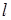 过
过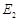 的上顶点时, 直线
的上顶点时, 直线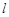 的倾斜角为
的倾斜角为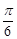 .
.
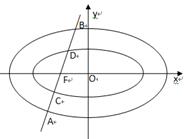
(1)求椭圆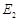 的方程;
的方程;
(2)求证: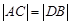 ;
;
(3)若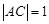 ,求直线
,求直线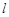 的方程.
的方程.
已知椭圆

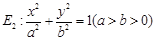 .
.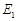 与
与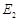 有相同的离心率,过点
有相同的离心率,过点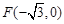 的直线
的直线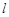 与
与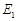 ,
,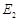 依次交于A,C,D,B四点(如图).当直线
依次交于A,C,D,B四点(如图).当直线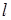 过
过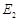 的上顶点时, 直线
的上顶点时, 直线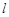 的倾斜角为
的倾斜角为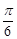 .
.
(1)求椭圆
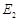 的方程;
的方程; (2)求证:
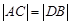 ;
; (3)若
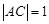 ,求直线
,求直线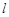 的方程.
的方程.解:(1)
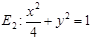 .(2)见解析;(3)
.(2)见解析;(3)
本试题主要是考查了椭圆方程的求解,以及利用直线与椭圆的位置关系求解直线的方程,证明线段相等的综合运用。
(1)利用椭圆的几何性质表示得到a,b,c的关系式,从而得到椭圆的方程。
(2)设直线与椭圆方程联系,借助于坐标的关系来证明相等即可。
(3)在第二问的基础上,进一步得到关于直线斜率k的表达式,化简得到直线的方程,
解:(1)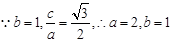 ,因此椭圆
,因此椭圆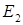 的方程为
的方程为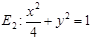 .
.
(2)当直线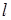 垂直
垂直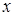 轴时,易求得
轴时,易求得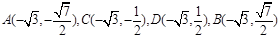
因此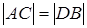 ,
,
当直线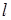 不垂直
不垂直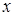 轴时,设
轴时,设
由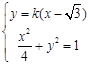
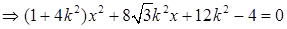 ①,
①,
由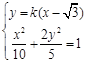
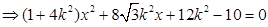 ②,
②,
设 ,则
,则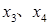 是方程①的解,
是方程①的解, 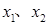 是方程②的解.
是方程②的解. ,
, 线段AB,CD的中点重合,
线段AB,CD的中点重合,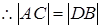
(3).由(2)知,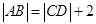 ,当直线
,当直线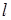 垂直
垂直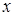 轴时,不合要求;
轴时,不合要求;
当直线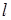 不垂直
不垂直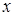 轴时,设
轴时,设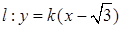 ,由(2)知,
,由(2)知,
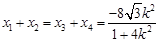 ,
,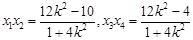 ,
,

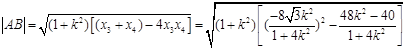
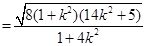
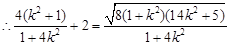 ,化简可得:
,化简可得:
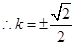 ,
,
(1)利用椭圆的几何性质表示得到a,b,c的关系式,从而得到椭圆的方程。
(2)设直线与椭圆方程联系,借助于坐标的关系来证明相等即可。
(3)在第二问的基础上,进一步得到关于直线斜率k的表达式,化简得到直线的方程,
解:(1)
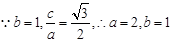 ,因此椭圆
,因此椭圆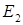 的方程为
的方程为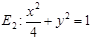 .
.(2)当直线
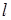 垂直
垂直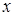 轴时,易求得
轴时,易求得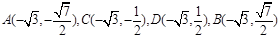
因此
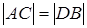 ,
,当直线
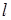 不垂直
不垂直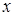 轴时,设
轴时,设
由
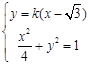
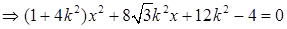 ①,
①,由
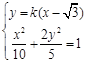
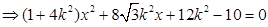 ②,
②,设
 ,则
,则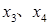 是方程①的解,
是方程①的解, 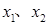 是方程②的解.
是方程②的解. ,
, 线段AB,CD的中点重合,
线段AB,CD的中点重合,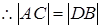
(3).由(2)知,
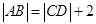 ,当直线
,当直线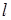 垂直
垂直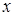 轴时,不合要求;
轴时,不合要求;当直线
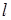 不垂直
不垂直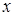 轴时,设
轴时,设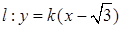 ,由(2)知,
,由(2)知,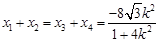 ,
,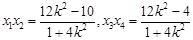 ,
,
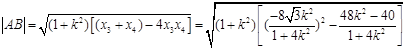
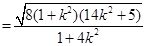
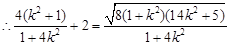 ,化简可得:
,化简可得:
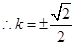 ,
,

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
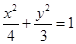 的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当
的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当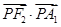 取最小值时,
取最小值时,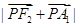 的值为( )
的值为( )


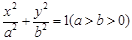 ,过右焦点且不与
,过右焦点且不与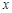 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于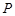 ,
,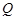 两点,若在椭圆的右准线上存在点
两点,若在椭圆的右准线上存在点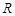 ,使
,使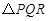 为正三角形,则椭圆的离心率的取值范围是 .
为正三角形,则椭圆的离心率的取值范围是 . 上的一点,点M、N分别是两圆:
上的一点,点M、N分别是两圆: 和
和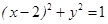 上的点,则的最小值、最大值分别为( )
上的点,则的最小值、最大值分别为( ) 的焦点与椭圆
的焦点与椭圆 的焦点重合,则此双曲线的离心率为
的焦点重合,则此双曲线的离心率为

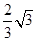

 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点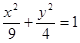 上一点
上一点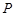 作圆
作圆 的两条切线,点
的两条切线,点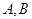 为切点.过
为切点.过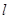 与
与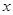 轴,
轴, 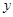 轴分别交于点
轴分别交于点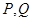 两点, 则
两点, 则 的面积的最小值为( )
的面积的最小值为( )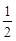
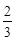
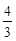
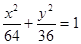 上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.
上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______. 有公共的焦点F1,F2,P是两曲线的一个交点,则
有公共的焦点F1,F2,P是两曲线的一个交点,则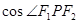 =( )
=( )