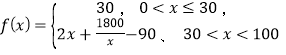题目内容
【题目】已知长方体![]() ,
,![]() ,
,![]() ,
,![]() ,已知P是矩形
,已知P是矩形![]() 内一动点,
内一动点,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,设P点形成的轨迹长度为
,设P点形成的轨迹长度为![]() ,则
,则![]() _________;当
_________;当![]() 的长度最短时,三棱锥
的长度最短时,三棱锥![]() 的外接球的表面积为_____________.
的外接球的表面积为_____________.
【答案】![]()
![]()
【解析】
先确定![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即得
,即得![]() ,从而根据弧长公式得
,从而根据弧长公式得![]() ,再根据二倍角正切公式得结果;先确定
,再根据二倍角正切公式得结果;先确定![]() 的长度最短时P点位置,再确定三棱锥
的长度最短时P点位置,再确定三棱锥![]() 的外接球的球心,根据
的外接球的球心,根据![]() 外接圆半径求得球半径,即得球的表面积.
外接圆半径求得球半径,即得球的表面积.
因为长方体![]() 中
中![]() 平面
平面![]() ,
,
所以![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
因为![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]()
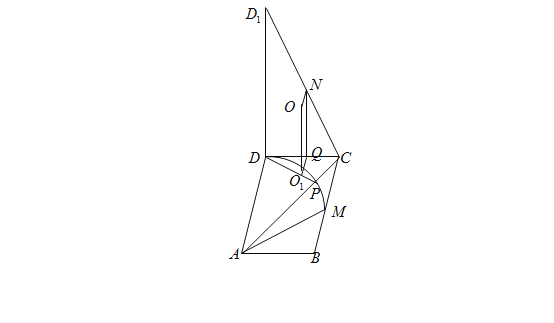
从而P点形成的轨迹为以A为圆心,2为半径的圆在矩形![]() 内一段圆弧
内一段圆弧![]() ,设其圆心角为
,设其圆心角为![]() ,则
,则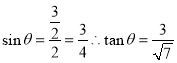
因此
因为![]() ,所以
,所以![]() 最小时,
最小时,![]() 长度最短,此时P为AC与上面圆弧
长度最短,此时P为AC与上面圆弧![]() 的交点,设
的交点,设![]() 外接圆圆心为
外接圆圆心为![]() ,半径为
,半径为![]() ,
,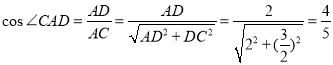
则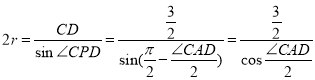
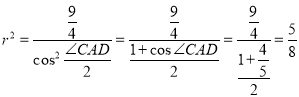
设三棱锥![]() 的外接球的球心为
的外接球的球心为![]() ,半径为
,半径为![]() ,
,
从而![]()
因此球的表面积为![]()
故答案为:![]() ;
;![]()

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目