��Ŀ����
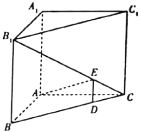
����Ŀ����ͼ���߳�Ϊ1������������OABC������OAΪ�뾶��Բ��![]() .�־�����AB����һ��D��һ���߶�DE��Բ��
.�־�����AB����һ��D��һ���߶�DE��Բ��![]() �����ڵ�E���Ӷ�������������OABC�ֳ����飺����COEΪ����I���ı���OADEΪ����II��ʣ�µ�CBDEΪ����III.����I������������II���ֻ�������III��ֲ��.ÿ��λƽ��������������������÷ֱ�Ϊ
�����ڵ�E���Ӷ�������������OABC�ֳ����飺����COEΪ����I���ı���OADEΪ����II��ʣ�µ�CBDEΪ����III.����I������������II���ֻ�������III��ֲ��.ÿ��λƽ��������������������÷ֱ�Ϊ![]() ��
��![]() ��
��![]() ���������W����
���������W����![]()

��1���ֱ���![]() ��ʾ����I��II��III�������
��ʾ����I��II��III�������
��2���������W��ʾΪ![]() �ĺ�������д��������
�ĺ�������д��������
��3����![]() Ϊ��ֵʱ�������Wȡ��Сֵ��
Ϊ��ֵʱ�������Wȡ��Сֵ��
���𰸡���1��![]() ��
��![]() ��
��![]() ��2��
��2��![]() ��������Ϊ
��������Ϊ![]() ��3��
��3��![]()
��������
��1�����������������ʽ�������I������IIΪ����ȫ�ȵ������Σ�����ֻ����![]() ��ʾ��
��ʾ��![]() �������������������������������II�����������III�ô���������������.��2������λ�����۷ֱ�������������ͣ������������ۣ�������֤ÿ���Ƕȴ����㼴��.��3�������������϶������������۵ĵ����ԣ��������������Сʱ��
�������������������������������II�����������III�ô���������������.��2������λ�����۷ֱ�������������ͣ������������ۣ�������֤ÿ���Ƕȴ����㼴��.��3�������������϶������������۵ĵ����ԣ��������������Сʱ��![]() ֵ.
ֵ.
�⣺(1)��ͼ��![]() ��
��
����OD����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() .
.
��2��![]() ��
��
��![]() ��֪
��֪![]() �����Ժ����Ķ�����Ϊ
�����Ժ����Ķ�����Ϊ![]()
(3) ![]() ��
��
��![]() ����
����![]() ��
��![]() ����ȥ��
����ȥ��
��![]() ������
������![]()
��![]() ʱ��
ʱ�� ![]() ��������
��������![]() �ϵ����ݼ���
�ϵ����ݼ���
��![]() ʱ��
ʱ��![]() ��������
��������![]() �ϵ���������
�ϵ���������
���Ե�![]() ʱ��
ʱ��![]() ȡ��Сֵ.
ȡ��Сֵ.
��![]() ʱ�������Wȡ��Сֵ��
ʱ�������Wȡ��Сֵ��

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�����Ŀ��![]() ���Ǵ�Ӯ���챣��ս�����ж��ƻ��ěQʤ֮�꣬���������ڸ��ظ����Ź�ͬŬ���£����챣��ս���������ʩ�Ȳ��ƽ���ȡ���˻�����Ч��ijѧ������ռ��˼׳��н������ϰ����и�
���Ǵ�Ӯ���챣��ս�����ж��ƻ��ěQʤ֮�꣬���������ڸ��ظ����Ź�ͬŬ���£����챣��ս���������ʩ�Ȳ��ƽ���ȡ���˻�����Ч��ijѧ������ռ��˼׳��н������ϰ����и�![]() ��Ŀ�����ָ��
��Ŀ�����ָ��![]() ���õ�Ƶ���ֲ������£�
���õ�Ƶ���ֲ������£�
![]() ���ϰ�����
���ϰ�����![]() ���
���![]() Ƶ���ֲ���
Ƶ���ֲ���
|
|
|
|
|
|
���� |
|
|
|
|
|
![]() ���ϰ�����
���ϰ�����![]() ���
���![]() Ƶ���ֲ���
Ƶ���ֲ���
|
|
|
|
|
|
���� |
|
|
|
|
|
��1������![]() ���ϰ���׳��п����������������ı�����
���ϰ���׳��п����������������ı�����
��2����![]() ���ϰ���׳���
���ϰ���׳���![]() ��ƽ�����ͱ���Ĺ���ֵ��ͬһ���е������ø���������е�ֵΪ������������ȷ��
��ƽ�����ͱ���Ĺ���ֵ��ͬһ���е������ø���������е�ֵΪ������������ȷ��![]() ��
��
��3������ѧ�Ľy��֪ʶ���Ƚ�![]() ���ϰ�����
���ϰ�����![]() ���ϰ���׳��еĿ����������.
���ϰ���׳��еĿ����������.
����
|
|
|
|
|
|
|
�������� | �� | �� | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ | ������Ⱦ |
![]() .
.