题目内容
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
【答案】(I)![]() .
.
(II)函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
【解析】试题分析:(Ⅰ)利用向量的数量积坐标运算公式代入函数式整理化简,将函数过的点![]() 和点
和点![]() 代入就可得到关于
代入就可得到关于![]() 的方程,解方程求其值;(Ⅱ)利用图像平移的方法得到
的方程,解方程求其值;(Ⅱ)利用图像平移的方法得到![]() 的解析式,利用最高点到点
的解析式,利用最高点到点![]() 的距离的最小值为1求得
的距离的最小值为1求得![]() 角,得
角,得![]() ,求减区间需令
,求减区间需令![]() 解
解![]() 的范围
的范围
试题解析:(1)由题意知![]() .
.
![]() 的过图象过点
的过图象过点![]() 和
和![]() ,
,
所以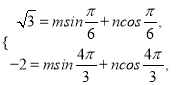 即
即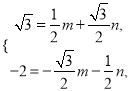 解得
解得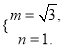
(2)由(1)知![]() .
.
由题意知![]() .
.
设![]() 的图象上符合题意的最高点为
的图象上符合题意的最高点为![]() ,
,
由题意知![]() ,所以
,所以![]() ,即到点(0,3)的距离为1的最高点为(0,2).
,即到点(0,3)的距离为1的最高点为(0,2).
将其代入![]() 得
得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因此![]() .
.
由![]() Z得
Z得![]() Z,
Z,
所以函数![]() 的单调递增区间为
的单调递增区间为![]()

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目