题目内容
【题目】已知函数f(x)=x2-1,g(x)=![]()
(1)求f[g(2)]和g[f(2)]的值;
(2)求f[g(x)]和g[f(x)]的表达式.
【答案】(1)0 2
(2)f[g(x)]=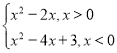
g[f(x)]=![]()
【解析】解:(1)由已知,g(2)=1,f(2)=3,
∴f[g(2)]=f(1)=0,g[f(2)]=g(3)=2.
(2)当x>0时,g(x)=x-1,故f[g(x)]=(x-1)2-1=x2-2x;
当x<0时,g(x)=2-x,故f[g(x)]=(2-x)2-1=x2-4x+3;
∴f[g(x)]=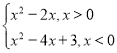
当x>1或x<-1时,f(x)>0,故g[f(x)]=f(x)-1=x2-2;
当-1<x<1时,f(x)<0,故g[f(x)]=2-f(x)=3-x2.
∴g[f(x)]=![]()

练习册系列答案
相关题目