题目内容
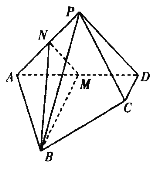
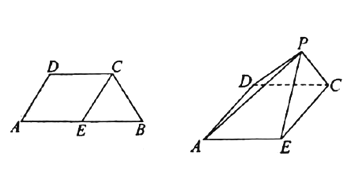
【题目】在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.现将
的中点.现将![]() 沿线段
沿线段![]() 翻折,得四棱锥
翻折,得四棱锥![]() ,且二面角
,且二面角![]() 为直二面角.
为直二面角.
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,通过等边三角形的性质得到
,通过等边三角形的性质得到![]() ,
,![]() ,根据线面垂直判定定理得到
,根据线面垂直判定定理得到![]() 平面
平面![]() ,故而可得结论;(2)由面面垂直性质定理可得
,故而可得结论;(2)由面面垂直性质定理可得![]() 平面
平面![]() ,求出平面
,求出平面![]() 的法向量为
的法向量为![]() ,同时
,同时![]() 是平面
是平面![]() 的一个法向量,求出法向量夹角的余弦值,进而可得结果.
的一个法向量,求出法向量夹角的余弦值,进而可得结果.
(1)如图连接![]() ,易知
,易知![]() ,
,![]() 均为正三角形,取
均为正三角形,取![]() 中点
中点![]() ,
,
连接![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)因为二面角![]() 为直二面角,所以平面
为直二面角,所以平面![]() 平面
平面![]() ,
,
又因为平面![]() 平面
平面![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() ,故以点
,故以点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.

则![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() .由
.由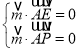 得
得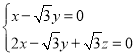
取![]() ,所以
,所以![]() .
.
又因为直线![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以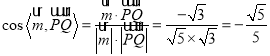 .
.
又因为二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值
的余弦值![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公司对4月份员工的奖金情况统计如下:
奖金(单位:元) | 8000 | 5000 | 4000 | 2000 | 1000 | 800 | 700 | 600 | 500 |
员工(单位:人) | 1 | 2 | 4 | 6 | 12 | 8 | 20 | 5 | 2 |
根据上表中的数据,可得该公司4月份员工的奖金:①中位数为800元;②平均数为1373元;③众数为700元,其中判断正确的个数为( )
A.0B.1C.2D.3
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
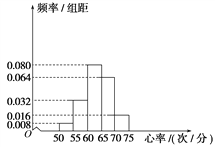
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |