题目内容
异面直线a，b所成的角为60°，过空间点P作线c与它们都成60°，则线c的条数为______．
过P作a'∥a，b'∥b，设直线a'、b'确定的平面为α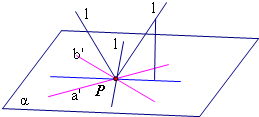
，
∵异面直线a、b成60°角，∴直线a'、b'所成锐角为60°．
①当直线l在平面α内时，
若直线l平分直线a'、b'所成的钝角，
则直线l与a、b都成60°角；
②当直线l与平面α斜交时，
若它在平面α内的射影恰好落在
直线a'、b'所成的锐角平分线上时，直线l与a、b所成角相等．
此时l与a'、b'所成角的范围为[30°，90°]，
适当调整l的位置，可使直线l与a、b也都成60°角，这样的直线l有两条．
综上所述，过点P与a'、b'都成60°角的直线，可以作3条
∵a'∥a，b'∥b，
∴过点P与a'、b'都成60°角的直线，与a、b也都成60°的角．
故答案为：3
，∵异面直线a、b成60°角，∴直线a'、b'所成锐角为60°．
①当直线l在平面α内时，
若直线l平分直线a'、b'所成的钝角，
则直线l与a、b都成60°角；
②当直线l与平面α斜交时，
若它在平面α内的射影恰好落在
直线a'、b'所成的锐角平分线上时，直线l与a、b所成角相等．
此时l与a'、b'所成角的范围为[30°，90°]，
适当调整l的位置，可使直线l与a、b也都成60°角，这样的直线l有两条．
综上所述，过点P与a'、b'都成60°角的直线，可以作3条
∵a'∥a，b'∥b，
∴过点P与a'、b'都成60°角的直线，与a、b也都成60°的角．
故答案为：3
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
