题目内容
4.设a为常数,记函数$f(x)=k{(\frac{x-1}{x+1})^2}$,x>1的反函数为f-1(x).已知y=f-1(x)的图象经过点$(\frac{1}{4},3)$.(Ⅰ)求实数k的值和反函数f-1(x)的解析式;
(Ⅱ)定义函数$F(x)={log_c}[{f^{-1}}(x)]-{log_c}\frac{{c-\sqrt{x}}}{{1-\sqrt{x}}}$,其中常数c>0且c≠1,求函数F(x)的值域.
分析 (Ⅰ)由y=f-1(x)的图象经过点$(\frac{1}{4},3)$,得到关于k的等式,求出实数k的值,进一步求得反函数f-1(x)的解析式;
(Ⅱ)把f-1(x)的解析式代入$F(x)={log_c}[{f^{-1}}(x)]-{log_c}\frac{{c-\sqrt{x}}}{{1-\sqrt{x}}}$,化简整理后求出真数的范围,可得函数的值域.
解答 解:(Ⅰ)∵$f(x)=k{(\frac{x-1}{x+1})^2}$,且y=f-1(x)的图象经过点$(\frac{1}{4},3)$,
∴$k(\frac{3-1}{3+1})^{2}=\frac{1}{4}$,解得k=1,
∴$y=f(x)=(\frac{x-1}{x+1})^{2}$(x>1),则$\frac{x-1}{x+1}=\sqrt{y}$,$x=\frac{1+\sqrt{y}}{1-\sqrt{y}}$.
∴${f}^{-1}(x)=\frac{1+\sqrt{x}}{1-\sqrt{x}}$(0<x<1);
(Ⅱ)$F(x)={log_c}[{f^{-1}}(x)]-{log_c}\frac{{c-\sqrt{x}}}{{1-\sqrt{x}}}$=$lo{g}_{c}\frac{1+\sqrt{x}}{1-\sqrt{x}}-lo{g}_{c}\frac{c-\sqrt{x}}{1-\sqrt{x}}$
=$lo{g}_{c}\frac{1+\sqrt{x}}{c-\sqrt{x}}$(0<x<1).
要使该函数有意义,则c-$\sqrt{x}>0$恒成立,
∵0<x<1,∴c>1.
由t=$\frac{1+\sqrt{x}}{c-\sqrt{x}}=-\frac{\sqrt{x}+1}{\sqrt{x}-c}=-\frac{\sqrt{x}-c+c+1}{\sqrt{x}-c}$=$-\frac{c+1}{\sqrt{x}-c}-1$,
∵0<x<1,∴0$<\sqrt{x}<1$,$-c<\sqrt{x}-c<1-c$,
∴$\frac{1}{1-c}<\frac{1}{\sqrt{x}-c}<\frac{1}{-c}$,$\frac{c+1}{c}<\frac{1+\sqrt{x}}{c-\sqrt{x}}<\frac{2}{c-1}$.
∴函数F(x)的值域为[$lo{g}_{c}\frac{c+1}{c},lo{g}_{c}\frac{2}{c-1}$].
点评 本题考查函数的性质,考查了函数反函数的求法,训练了函数值域的求法,是中档题.

| A. | y=tanx | B. | y=sinx | C. | $y={x^{\frac{1}{3}}}$ | D. | $y={x^{\frac{1}{2}}}$ |
| A. | 4个 | B. | 3 个 | C. | 2 个 | D. | 1 个 |
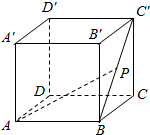 如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.
如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.