题目内容
设椭圆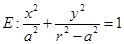 的焦点在
的焦点在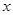 轴上,
轴上, 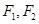 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点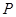 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线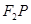 交
交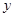 轴于点
轴于点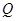 ,
,
(1)当 时,
时,
(1)若椭圆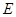 的离心率为
的离心率为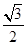 ,求椭圆
,求椭圆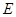 的方程;
的方程;
(2)当点P在直线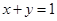 上时,求直线
上时,求直线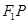 与
与 的夹角;
的夹角;
(2) 当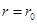 时,若总有
时,若总有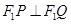 ,猜想:当
,猜想:当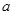 变化时,点
变化时,点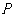 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).
(1)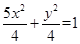 ,
,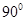 (2)
(2)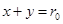 .
.
解析试题分析:本题主要考查椭圆的标准方程、直线的方程、两直线垂直的充要条件等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,(ⅰ)利用椭圆的定义及离心率列出方程,得到椭圆方程中的基本量a,b,从而得到椭圆的标准方程;(ⅱ)设出P点坐标、设出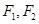 点坐标,点P在椭圆上且在直线
点坐标,点P在椭圆上且在直线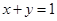 上,得到
上,得到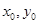 的值,从而得到
的值,从而得到 和
和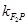 ,由于Q点是直线
,由于Q点是直线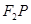 与y轴的交点,所以先得到直线
与y轴的交点,所以先得到直线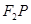 的方程,再得到Q点坐标,从而得到
的方程,再得到Q点坐标,从而得到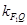 ,由于
,由于 ,所以判断F1P⊥F1Q;第二问,由第(ⅱ)问的证明,可以猜想方程
,所以判断F1P⊥F1Q;第二问,由第(ⅱ)问的证明,可以猜想方程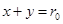 .
.
试题解析:(1)(1) 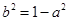 ,
,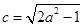 ,
,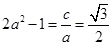 ,解得
,解得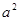 =
=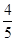 .故椭圆E的方程为
.故椭圆E的方程为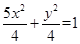 . 4分
. 4分
(2)设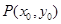 ,
,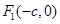
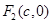 ,,其中
,,其中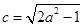 .由题设知
.由题设知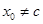 ,
,
将直线 代入椭圆E的方程,由于点
代入椭圆E的方程,由于点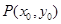 在第一象限,解得
在第一象限,解得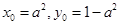 6分
6分
则直线F1P的斜率 =
= ,直线F2P的斜率
,直线F2P的斜率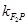 =
= ,
,
故直线F2P的方程为y=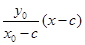 .当x=0时,y=
.当x=0时,y=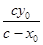 ,
,
即点Q坐标为 .因此,直线F1Q的斜率为
.因此,直线F1Q的斜率为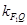 =
=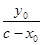 .
.
所以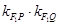 =
=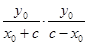 =-1.
=-1.
所以F1P⊥F1Q, 10分
(2)点P过定直线,方程为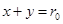 13分
13分
考点:椭圆的标准方程、直线的方程、两直线垂直的充要条件.

练习册系列答案
相关题目
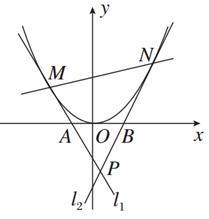
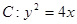 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.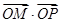 为定值;
为定值;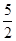 ,求向量
,求向量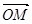 与
与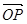 的夹角;
的夹角;
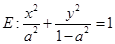 的焦点在
的焦点在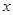 轴上.
轴上.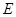 的焦距为1,求椭圆
的焦距为1,求椭圆 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 交
交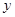 轴与点
轴与点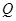 ,并且
,并且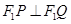 ,证明:当
,证明:当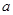 变化时,点
变化时,点 在某定直线上.
在某定直线上.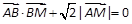 ,
,
 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .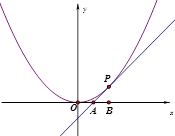
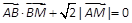 ,求点M的轨迹C;
,求点M的轨迹C; 的焦点
的焦点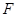 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证: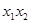 为定值;
为定值;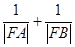 为定值.
为定值.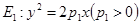 和
和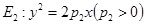 ,过原点
,过原点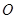 的两条直线
的两条直线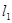 和
和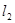 ,
, 分别交于
分别交于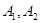 两点,
两点,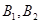 两点.
两点.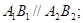
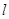 (异于
(异于 两点.记
两点.记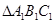 与
与 的面积分别为
的面积分别为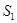 与
与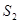 ,求
,求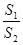 的值.
的值.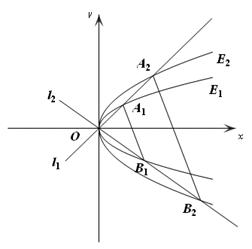
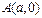 和
和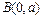 的直线与抛物线
的直线与抛物线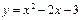 没有交点,那么实数
没有交点,那么实数 的取值范围是
的取值范围是