题目内容
已知椭圆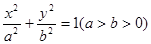 的右焦点为
的右焦点为 ,
, 为上顶点,
为上顶点,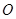 为坐标原点,若△
为坐标原点,若△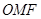 的面积为
的面积为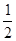 ,且椭圆的离心率为
,且椭圆的离心率为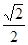 .
.
(1)求椭圆的方程;
(2)是否存在直线 交椭圆于
交椭圆于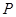 ,
, 两点, 且使点
两点, 且使点 为△
为△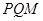 的垂心?若存在,求出直线
的垂心?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)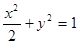 ;(2)存在直线
;(2)存在直线 ,且直线
,且直线 的方程为
的方程为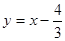 .
.
解析试题分析:(1)由题意可得 的两个关系式即
的两个关系式即 ,解之即可得椭圆的方程;(2)先假设存在直线
,解之即可得椭圆的方程;(2)先假设存在直线 与椭圆交于
与椭圆交于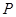 ,
, 两点,且椭圆的右焦点
两点,且椭圆的右焦点 恰为
恰为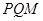 的垂心.设出
的垂心.设出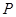 ,
, 坐标,由(1)中所求椭圆方程,可得
坐标,由(1)中所求椭圆方程,可得 ,
, 点坐标,利用点
点坐标,利用点 恰为
恰为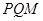 的垂心,则
的垂心,则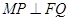 ,就可得到含
,就可得到含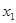 ,
,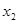 ,
, ,
,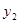 的等式,再设直线
的等式,再设直线 的方程为
的方程为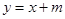 ,代入椭圆方程,求
,代入椭圆方程,求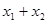 ,
,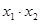 ,
, ,
,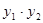 ,均用含
,均用含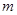 的式子表示,再代入上面所求等式中,求
的式子表示,再代入上面所求等式中,求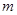 ,若能求出,则存在直线
,若能求出,则存在直线 与椭圆交于
与椭圆交于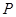 ,
, 两点,且椭圆的右焦点
两点,且椭圆的右焦点 恰为
恰为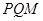 的垂心,若求不出,则不存在直线
的垂心,若求不出,则不存在直线 与椭圆交于
与椭圆交于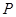 ,
, 两点,且椭圆的右焦点
两点,且椭圆的右焦点 恰为
恰为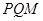 的垂心.
的垂心.
试题解析:(1)由题意可得 ,解得
,解得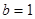 ,
,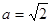 ,故椭圆方程为
,故椭圆方程为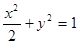 .
.
(2)假设存在直线 交椭圆于
交椭圆于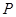 ,
, 两点,且
两点,且 为△
为△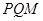 的垂心,设
的垂心,设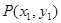 ,
,
因为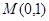 ,
,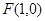 ,故
,故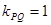 .于是设直线
.于是设直线 的方程为
的方程为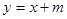 ,
,
由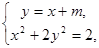 得
得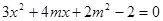 .
.
由 ,得
,得 , 且
, 且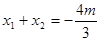 ,
,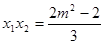 .
.
由题意应有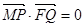 ,又
,又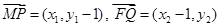 ,
,
故 ,得
,得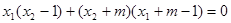 .
.
即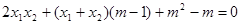 .
.
整理得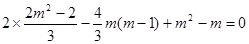 .
.
解得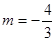 或
或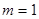 .经检验,当
.经检验,当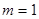 时,△
时,△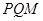 不存在,故舍去
不存在,故舍去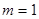 .
.
当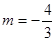 时,所求直线
时,所求直线 存在,且直线
存在,且直线 的方程为
的方程为
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
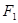 和
和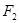 ,且|
,且|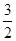 )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若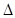 A
A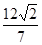 ,求以
,求以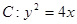 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.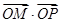 为定值;
为定值;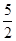 ,求向量
,求向量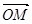 与
与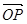 的夹角;
的夹角;
 ,直线l过定点
,直线l过定点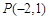 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?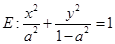 的焦点在
的焦点在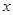 轴上.
轴上.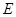 的焦距为1,求椭圆
的焦距为1,求椭圆 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 交
交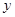 轴与点
轴与点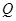 ,并且
,并且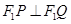 ,证明:当
,证明:当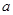 变化时,点
变化时,点 在某定直线上.
在某定直线上.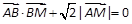 ,
, 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .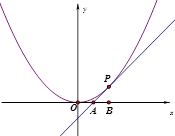
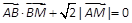 ,求点M的轨迹C;
,求点M的轨迹C; 中,点
中,点 到点
到点 的距离比它到
的距离比它到 轴的距离多1,记点
轴的距离多1,记点 .
. 的直线
的直线 过定点
过定点 ,求直线
,求直线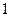 的直线
的直线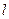 与椭圆
与椭圆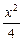 +y2=1相交于A、B两点,则|AB|的最大值为
+y2=1相交于A、B两点,则|AB|的最大值为