题目内容
已知椭圆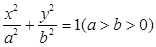 经过点
经过点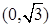 ,离心率为
,离心率为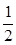 ,左右焦点分别为
,左右焦点分别为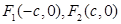 .
.
(1)求椭圆的方程;
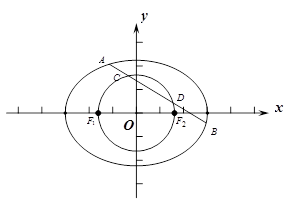
(2)若直线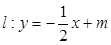 与椭圆交于
与椭圆交于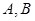 两点,与以
两点,与以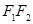 为直径的圆交于
为直径的圆交于 两点,且满足
两点,且满足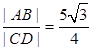 ,求直线
,求直线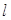 的方程.
的方程.
(1)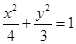 ;(2)
;(2) 或
或 .
.
解析试题分析:(1)由题意可得 ,解出
,解出 ,
,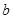 的值,即可求出椭圆的方程;
的值,即可求出椭圆的方程;
(2)由题意可得以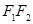 为直径的圆的方程为
为直径的圆的方程为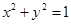 ,利用点到直线的距离公式得:圆心到直线
,利用点到直线的距离公式得:圆心到直线 的距离
的距离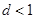 ,可得
,可得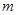 的取值范围,利用弦长公式可得
的取值范围,利用弦长公式可得 ,设
,设 ,把直线
,把直线 的方程与椭圆的方程联立可得根与系数的关系,进而得到弦长
的方程与椭圆的方程联立可得根与系数的关系,进而得到弦长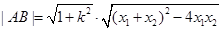 ,由
,由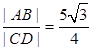 ,即可解得
,即可解得 的值.
的值.
试题解析:(1)由题意可得
解得
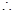 椭圆的方程为
椭圆的方程为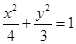
由题意可得以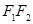 为直径的圆的方程为
为直径的圆的方程为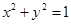
 圆心到直线
圆心到直线 的距离为
的距离为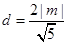
由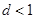 ,即
,即 ,可得
,可得

设
联立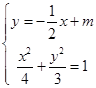
整理得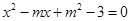
可得: ,
,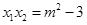


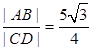

解方程得 ,且满足
,且满足
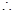 直线
直线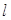 的方程为
的方程为 或
或
考点:椭圆的标准方程;直线与圆锥曲线的综合问题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
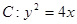 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.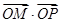 为定值;
为定值;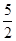 ,求向量
,求向量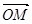 与
与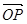 的夹角;
的夹角;
 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .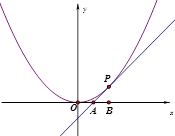
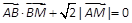 ,求点M的轨迹C;
,求点M的轨迹C; 的焦点
的焦点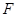 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证: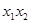 为定值;
为定值;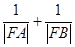 为定值.
为定值. 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且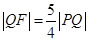 .
.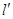 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程. 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知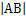 =
=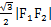 .
.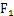 ,经过点
,经过点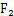 的直线
的直线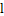 与该圆相切与点M,
与该圆相切与点M,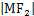 =
=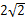 .求椭圆的方程.
.求椭圆的方程. 中,点
中,点 到点
到点 的距离比它到
的距离比它到 轴的距离多1,记点
轴的距离多1,记点 .
. 的直线
的直线 过定点
过定点 ,求直线
,求直线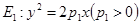 和
和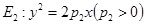 ,过原点
,过原点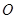 的两条直线
的两条直线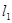 和
和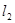 ,
, 分别交于
分别交于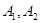 两点,
两点,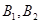 两点.
两点.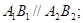
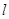 (异于
(异于 两点.记
两点.记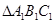 与
与 的面积分别为
的面积分别为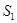 与
与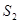 ,求
,求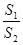 的值.
的值.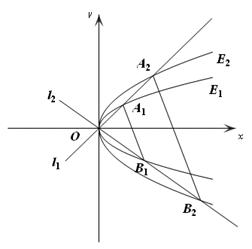
 :
: 的左顶点为
的左顶点为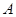 ,直线
,直线 交椭圆
交椭圆 两点(
两点( 上
上 下),动点
下),动点 和定点
和定点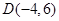 都在椭圆
都在椭圆 的面积.
的面积. 为梯形,求点
为梯形,求点 为实数,
为实数, ,求
,求 的最大值.
的最大值.