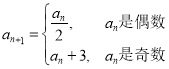题目内容
【题目】甲、乙两地相距300千米，汽车从甲地匀速行驶到乙地，速度不超过100千米/小时，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成，可变部分与速度
（千米/小时）的平方成正比，比例系数为
（
），固定部分为1000元.
（1）把全程运输成本
（元）表示为速度（千米/小时）的函数，并指出这个函数的定义域；
（2）为了使全程运输成本最小，汽车应以多大速度行驶？
【答案】（1）
，
；
（2）当
时，
，
时，
时最小.
【解析】
(1)全程运输成本有两部分组成,将其分别表示出来依题意建立起全程运输成本
(元)表示为速度
(千米/时)的倍数,由题设条件速度不得超过70千米/时,故定义域为
;
(2)由(1)知,全程运输成本关于速度的函数表达式中出现了积为定值的情形，由于等号成立的条件有可能不成立,故求最值的方法不确定，对速度的范围进行分类讨论
解：（1）由题意得，全程运输成本
，
（2）因为
所以
当且仅当
时取等号，即
① 当
时，即时
时，最小
② 当
时，即
时，在
上单调递减
则时，
最小
练习册系列答案
相关题目
