题目内容
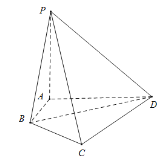
【题目】一胸针图样由等腰三角形![]() 及圆心
及圆心![]() 在中轴线上的圆弧
在中轴线上的圆弧![]() 构成,已知
构成,已知![]() ,
,![]() .为了增加胸针的美观程度,设计师准备焊接三条金丝线
.为了增加胸针的美观程度,设计师准备焊接三条金丝线![]() 且
且![]() 长度不小于
长度不小于![]() 长度,设
长度,设![]() .
.

(1)试求出金丝线的总长度![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,金丝线的总长度
为何值时,金丝线的总长度![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
【答案】(1)![]() ,[
,[![]() ,
,![]() );(2)
);(2)![]() ,
,![]()
【解析】
(1)由题可知,![]() ,
,![]() ,从而得出
,从而得出![]() ,
,![]() ,在
,在![]() 中,根据正弦定理即可求出
中,根据正弦定理即可求出![]() 和
和![]() ,即可金丝线的总长度
,即可金丝线的总长度![]() ,再根据
,再根据![]() 长度不小于
长度不小于![]() 长度,即可求出
长度,即可求出![]() 的取值范围;
的取值范围;
(2)由(1)得![]() 且
且![]() ,根据三角函数的图象和性质,即可求出
,根据三角函数的图象和性质,即可求出![]() 的最小值.
的最小值.
解:(1)∵圆心![]() 在中轴线上,
在中轴线上,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
根据正弦定理得:![]() ,
,
得![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 长度不小于
长度不小于![]() 长度,即
长度,即![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() ,解得:
,解得:![]() ,
,
∴![]() 的取值范围是[
的取值范围是[![]() ,
,![]() ).
).
(2)由(1)得![]() ,
,![]() ,
,
∴![]() ,此时
,此时![]() 单调递增,
单调递增,
∴当![]() ,即
,即![]() 时,
时,![]() 取得最小值,为
取得最小值,为![]() ,
,
此时金丝线的总长度![]() 最小,最小值为
最小,最小值为![]() ,
,
∴当![]() 时,金丝线的总长度
时,金丝线的总长度![]() 最小,
最小,![]() 的最小值是
的最小值是![]() .
.

练习册系列答案
相关题目