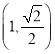题目内容
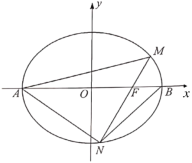
【题目】如图,点![]() 分别为椭圆
分别为椭圆![]() 的左右顶点和右焦点,过点
的左右顶点和右焦点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
(1)若![]() ,点
,点![]() 与椭圆
与椭圆![]() 左准线的距离为
左准线的距离为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 的斜率是直线
的斜率是直线![]() 斜率的
斜率的![]() 倍.
倍.
①求椭圆![]() 的离心率;
的离心率;
②若椭圆![]() 的焦距为
的焦距为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() .(2)①
.(2)①![]() ;②
;②![]()
【解析】
由所给条件列出关于![]() 的式子,求出椭圆方程;(2)①方法一,首先利用点在椭圆上,求得
的式子,求出椭圆方程;(2)①方法一,首先利用点在椭圆上,求得![]() ,再利用直线
,再利用直线![]() 方程与椭圆方程联立,求得
方程与椭圆方程联立,求得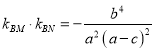 ,再利用
,再利用![]() 的关系,求得椭圆离心率;方法二,利用
的关系,求得椭圆离心率;方法二,利用![]() 的关系,分别设直线
的关系,分别设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,解出点
,与椭圆方程联立,解出点![]() 的坐标,利用点
的坐标,利用点![]() 三点共线,求得离心率.②首先求得椭圆方程,并表示
三点共线,求得离心率.②首先求得椭圆方程,并表示![]() 面积
面积![]() ,由①方法一,代入根与系数的关系,求
,由①方法一,代入根与系数的关系,求![]() 面积的最大值.
面积的最大值.
(1)∵![]() ,点
,点![]() 与椭圆
与椭圆![]() 左准线的距离为
左准线的距离为![]() ,
,
∴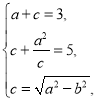 解得
解得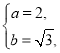
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)①法一:显然![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
则∵点![]() 在椭圆
在椭圆![]() 上,∴
上,∴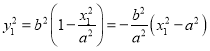 ,
,
∴![]() (i),
(i),
设直线![]() ,
,
与椭圆![]() 联立方程组消去
联立方程组消去![]() 得:
得:
![]() ,其两根为
,其两根为![]() ,
,
∴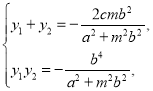 (*)
(*)
∴![]()
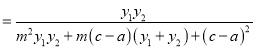 ,
,
将(*)代入上式化简得: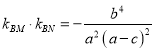 (ii)
(ii)
又![]() (iii)
(iii)
由(i)(ii)(iii)得: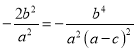 ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() ,即椭圆
,即椭圆![]() 的离心率为
的离心率为![]() .
.
法二:显然![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴设直线
,∴设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
由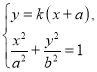 得
得![]() ,
,
注意到其一根为![]() ,∴另一根为
,∴另一根为![]() ,
,
∴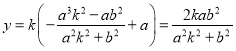 ,即
,即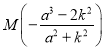 ,
,
同理由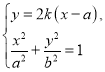 得
得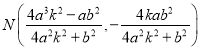 .
.
由![]() 三点共线得
三点共线得![]() ,
,
∴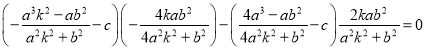 ,
,
化简得:![]() ,∴
,∴![]() ,
,
∴![]() ,即椭圆
,即椭圆![]() 的离心率为
的离心率为![]() .
.
②由①![]() ,又椭圆
,又椭圆![]() 的焦距为
的焦距为![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由①方法一得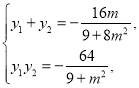
∴![]() 面积
面积![]()
![]() ,
,![]()
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∵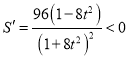 ,∴
,∴![]() 在
在![]() 为减函数,
为减函数,
∴![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目