题目内容
(本小题满分14分)
设正整数数列{an}满足:a2=4,且对于任何
n∈N*,有 .
.
(1)求a1,a3;
(2)求数列{ an }的通项an.
设正整数数列{an}满足:a2=4,且对于任何
n∈N*,有
 .
.(1)求a1,a3;
(2)求数列{ an }的通项an.
(1)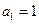 ,
,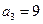
(2)对任意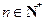 ,
,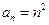
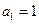 ,
,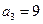
(2)对任意
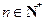 ,
,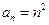
解:(1)据条件得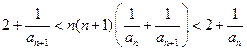 ①
①
当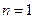 时,由
时,由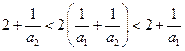 ,即有
,即有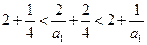 ,
,
解得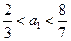 .因为
.因为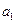 为正整数,故
为正整数,故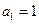 .
.
当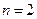 时,由
时,由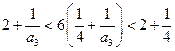 ,
,
解得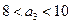 ,所以
,所以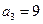 .
.
(2)方法一:由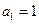 ,
,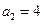 ,
,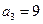 ,猜想:
,猜想: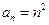 .
.
下面用数学归纳法证明.
1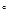 当
当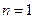 ,
,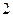 时,由(1)知
时,由(1)知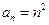 均成立;
均成立;
2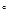 假设
假设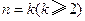 成立,则
成立,则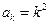 ,则
,则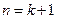 时
时
由①得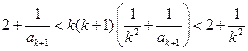
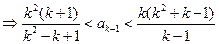

因为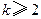 时,
时,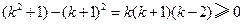 ,所以
,所以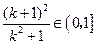 .
.
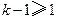 ,所以
,所以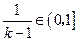 .
.
又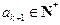 ,所以
,所以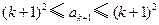 .
.
故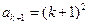 ,即
,即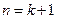 时,
时,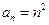 成立.
成立.
由1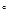 ,2
,2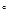 知,对任意
知,对任意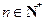 ,
,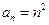 .
.
(2)方法二:
由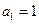 ,
,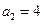 ,
,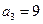 ,猜想:
,猜想: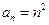 .
.
下面用数学归纳法证明.
1 当
当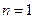 ,
,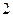 时,由(1)知
时,由(1)知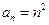 均成立;
均成立;
2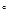 假设
假设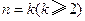 成立,则
成立,则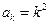 ,则
,则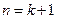 时
时
由①得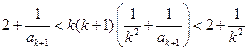
即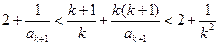 ②
②
由②左式,得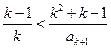 ,即
,即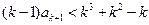 ,因为两端为整数,
,因为两端为整数,
则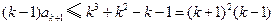 .于是
.于是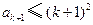 ③
③
又由②右式,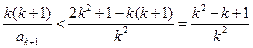 .
.
则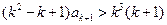 .
.
因为两端为正整数,则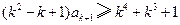 ,
,
所以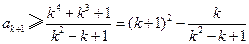 .
.
又因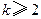 时,
时,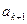 为正整数,则
为正整数,则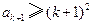 ④
④
据③④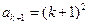 ,即
,即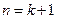 时,
时,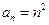 成立.
成立.
由1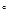 ,2
,2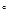 知,对任意
知,对任意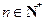 ,
,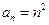 .
.
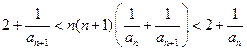 ①
①当
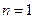 时,由
时,由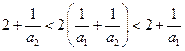 ,即有
,即有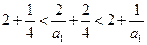 ,
,解得
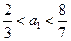 .因为
.因为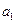 为正整数,故
为正整数,故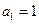 .
.当
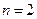 时,由
时,由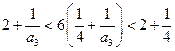 ,
,解得
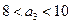 ,所以
,所以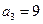 .
.(2)方法一:由
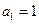 ,
,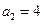 ,
,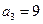 ,猜想:
,猜想: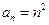 .
.下面用数学归纳法证明.
1
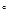 当
当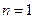 ,
,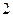 时,由(1)知
时,由(1)知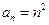 均成立;
均成立;2
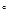 假设
假设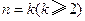 成立,则
成立,则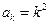 ,则
,则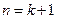 时
时由①得
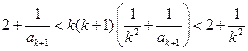
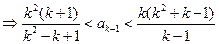

因为
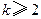 时,
时,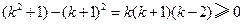 ,所以
,所以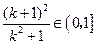 .
.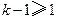 ,所以
,所以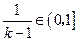 .
.又
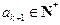 ,所以
,所以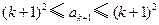 .
.故
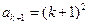 ,即
,即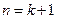 时,
时,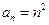 成立.
成立.由1
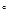 ,2
,2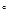 知,对任意
知,对任意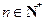 ,
,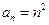 .
.(2)方法二:
由
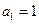 ,
,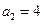 ,
,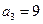 ,猜想:
,猜想: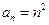 .
.下面用数学归纳法证明.
1
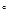 当
当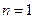 ,
,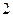 时,由(1)知
时,由(1)知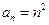 均成立;
均成立;2
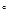 假设
假设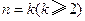 成立,则
成立,则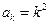 ,则
,则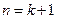 时
时由①得
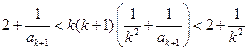
即
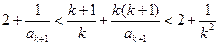 ②
②由②左式,得
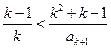 ,即
,即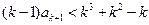 ,因为两端为整数,
,因为两端为整数,则
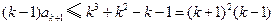 .于是
.于是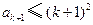 ③
③又由②右式,
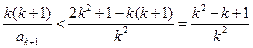 .
.则
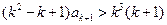 .
.因为两端为正整数,则
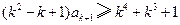 ,
,所以
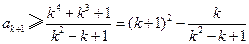 .
.又因
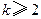 时,
时,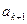 为正整数,则
为正整数,则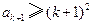 ④
④据③④
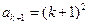 ,即
,即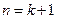 时,
时,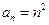 成立.
成立.由1
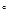 ,2
,2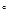 知,对任意
知,对任意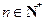 ,
,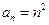 .
.
练习册系列答案
相关题目
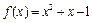 ,
,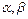 是方程f(x)=0的两个根
是方程f(x)=0的两个根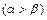 ,
,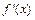 是f(x)的导数.
是f(x)的导数. ,
,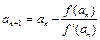 (n=1,2,……)
(n=1,2,……)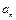 >a;
>a;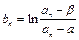 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。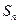 为数列
为数列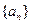 的前
的前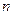 项和,
项和,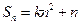 ,
,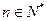 ,其中
,其中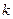 是常数.
是常数.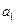 及
及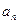 ;
;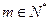 ,
,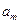 ,
,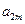 ,
,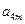 成等比数列,求
成等比数列,求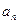 }满足
}满足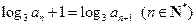 ,且
,且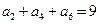 ,则
,则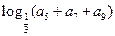 的值是
的值是 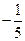
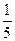
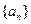 中,已知
中,已知 ,则该数列的前5项之和为( )
,则该数列的前5项之和为( ) )10 (
)10 ( )16 (
)16 ( )20 (
)20 ( )32
)32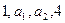 成等差数列,
成等差数列,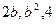 成等比数列,则
成等比数列,则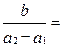 ( )
( )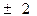
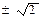

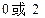
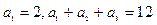
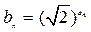 ,求数列{bn}的前10项和
,求数列{bn}的前10项和