题目内容
(本题满分14分)
已知函数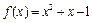 ,
,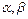 是方程f(x)=0的两个根
是方程f(x)=0的两个根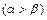 ,
,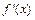 是f(x)的导数.
是f(x)的导数.
设 ,
,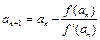 (n=1,2,……)
(n=1,2,……)
(1)求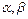 的值;
的值;
(2)证明:对任意的正整数n,都有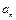 >a;
>a;
(3)记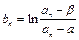 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。
已知函数
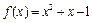 ,
,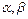 是方程f(x)=0的两个根
是方程f(x)=0的两个根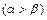 ,
,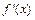 是f(x)的导数.
是f(x)的导数.设
 ,
,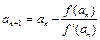 (n=1,2,……)
(n=1,2,……)(1)求
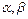 的值;
的值;(2)证明:对任意的正整数n,都有
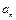 >a;
>a;(3)记
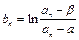 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。略
(1)解方程x2+x-1=0得x=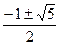
由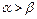 ?知?
?知?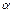 =
=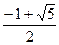 ,β=
,β=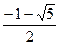
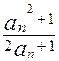
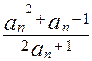
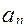 (2) f’ (x)=2x+1
(2) f’ (x)=2x+1
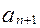 =" " - =" "
=" " - =" "
下面我们用数学归纳法来证明该结论成立
①当n=1时,a1=1<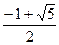 =?成立,
=?成立,
②假设n=k(k≥1, k∈N*)时,结论也成立,即ak<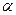 成立,
成立,
③那么当n=k+1时,
 =
=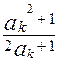 =
=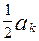 -
-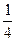 +
+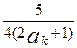 <
<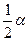 -
-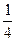 +
+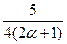 =
=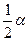 +
+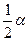 =
=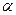
这就是说,当n=k+1时,结论也成立,故对于任意的正整数n,都有an<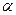
(3)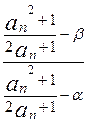
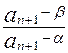 =" " =" " =
=" " =" " =
=(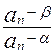 )2
)2
由题意知an>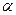 ,那么有an>β,于是对上式两边取对数得
,那么有an>β,于是对上式两边取对数得
ln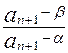 =ln(
=ln(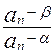 )2="2" ln(
)2="2" ln(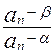 )
)
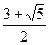 即数列{bn}为首项为b1= ln(
即数列{bn}为首项为b1= ln(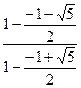 )="2ln( " ),公比为2的等比数列。
)="2ln( " ),公比为2的等比数列。
故其前n项和
Sn="2ln( " ) ="2ln( " )(2n -1).
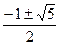
由
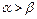 ?知?
?知?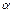 =
=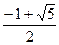 ,β=
,β=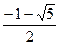
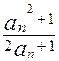
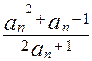
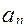 (2) f’ (x)=2x+1
(2) f’ (x)=2x+1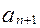 =" " - =" "
=" " - =" " 下面我们用数学归纳法来证明该结论成立
①当n=1时,a1=1<
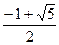 =?成立,
=?成立,②假设n=k(k≥1, k∈N*)时,结论也成立,即ak<
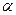 成立,
成立,③那么当n=k+1时,
 =
=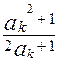 =
=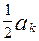 -
-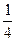 +
+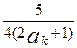 <
<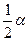 -
-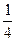 +
+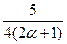 =
=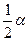 +
+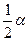 =
=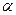
这就是说,当n=k+1时,结论也成立,故对于任意的正整数n,都有an<
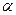
(3)
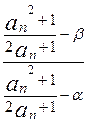
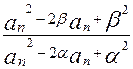 | |||
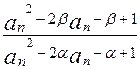 | |||
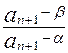 =" " =" " =
=" " =" " ==(
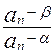 )2
)2由题意知an>
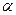 ,那么有an>β,于是对上式两边取对数得
,那么有an>β,于是对上式两边取对数得ln
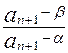 =ln(
=ln(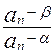 )2="2" ln(
)2="2" ln(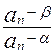 )
)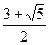 即数列{bn}为首项为b1= ln(
即数列{bn}为首项为b1= ln(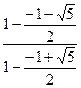 )="2ln( " ),公比为2的等比数列。
)="2ln( " ),公比为2的等比数列。故其前n项和
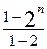 | |||||
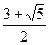 | |||||
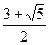 | |||||
Sn="2ln( " ) ="2ln( " )(2n -1).

练习册系列答案
相关题目
 .
. 12分)已知等差数列{an2
12分)已知等差数列{an2 }中,首项a12=1,公差d=1,an>0,n∈N
}中,首项a12=1,公差d=1,an>0,n∈N *.
*.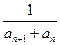 ,数列{bn}的前120项和T120;
,数列{bn}的前120项和T120; 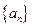 的前
的前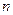 项和为
项和为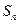 ,且满足
,且满足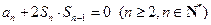 ,
,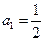 .
.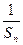 }是等差数列;
}是等差数列;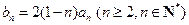 ,求证:
,求证: 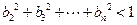 .
.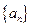 的通项公式为
的通项公式为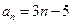 ,则
,则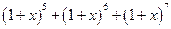 的展开式中含
的展开式中含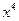 项的系数是该数列的
项的系数是该数列的  ( )
( )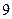 项
项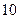 项
项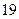 项
项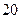 项
项 的等差数列
的等差数列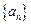 的前
的前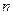 项和为
项和为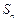 ,若
,若 则
则 =( )
=( )
 已知等差数列前三项为
已知等差数列前三项为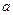 ,4,3
,4,3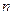 项和
项和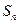 ,若
,若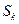 =2550。
=2550。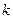 的值;(2)求
的值;(2)求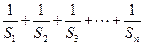 。
。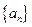 中,
中,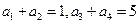 ,那么
,那么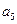 = .
= .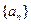 的通项
的通项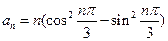 ,其前
,其前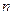 项和为
项和为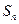 ,则
,则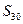 =____★____.
=____★____.