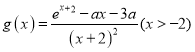题目内容
【题目】集合A={x||x+1|＜4}，B={x|（x﹣1）（x﹣2a）＜0}．
（1）求A，B；
（2）若A∩B=B，求实数a的取值范围．
【答案】
（1）解：A={x||x+1|＜4}={x|﹣5＜x＜3}，
当a＞0.5时，B={x|1＜x＜2a}．
当a=0.5时，B=．
当a＜0.5时，B={x|2a＜x＜1}
（2）解：由（1）知，A={x|﹣5＜x＜3}，
∵A∩B=B，
∴BA，
①当a＞0.5时，B={x|1＜x＜2a}．
此时， 
，则 
＜a≤1.5；
②当a=0.5时，B=．满足题意；
③当a＜0.5时，B={x|2a＜x＜1}．
此时 
，则﹣2.5≤a＜0.5．
综上所述，实数a的取值范围是[﹣2.5，1.5]
【解析】（1）通过解绝对值不等式得到集合A，对于集合B，需要对a的取值进行分类讨论：（2）A∩B=B，则B是A的子集，据此求实数a的取值范围．
练习册系列答案
相关题目
