题目内容
【题目】已知函数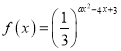 .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 有最大值
有最大值![]() ,求
,求![]() 的值.
的值.
【答案】(1)递增区间是![]() ,递减区间是
,递减区间是![]() .(2)3
.(2)3
【解析】试题分析:(1)根据复合函数单调性,先根据对称轴求二次函数单调性,再根据复合性研究单调区间(2)根据a讨论,函数单调性,再根据单调性确定函数最大值,最后根据方程解出![]() 的值.
的值.
试题解析:解:(1)当![]() 时,
时, ![]() ,对称轴为
,对称轴为![]() ,所以函数
,所以函数![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() .
.
(2)当![]() 时,
时, ![]() 单调递增,无最大值
单调递增,无最大值
当![]() 时,
时, ![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ,最大值为
,最大值为![]()
当![]() 时,
时, ![]() 递减区间是
递减区间是![]() ,递增区间是
,递增区间是![]() ,无最大值
,无最大值
综上![]()
点睛:1.复合函数单调性的规则
若两个简单函数的单调性相同,则它们的复合函数为增函数;若两个简单函数的单调性相反,则它们的复合函数为减函数.即“同增异减”.
2.函数单调性的性质
(1)若f(x),g(x)均为区间A上的增(减)函数,则f(x)+g(x)也是区间A上的增(减)函数,更进一步,即增+增=增,增-减=增,减+减=减,减-增=减;
(2)奇函数在其关于原点对称的区间上单调性相同,偶函数在其关于原点对称的区间上单调性相反.

【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |