题目内容
【题目】甲乙两人进行跳棋比赛，约定每局胜者得1分，负者得0分.若其中的一方比对方多得2分或下满5局时停止比赛.设甲在每局中获胜的概率为
，乙在每局中获胜的概率为
，且各局胜负相互独立.
（1）求没下满5局甲就获胜的概率；
（2）设比赛结束时已下局数为
，求的分布列及数学期望.
【答案】(1)
；(2)答案见解析.
【解析】试题分析：
（1）没下满
局甲就获胜有两种情况：①两局后甲获胜，此时
，②四局后甲获胜，此时
，则满足题意的概率值为
（2）由题意知
的所有取值为
：
，
，
，据此可得的分布列，计算其数学期望为
．
试题解析：
（1）没下满局甲就获胜有两种情况：
①两局后甲获胜，此时
，
②四局后甲获胜，此时
，
所以，没下满5局甲就获胜的概率
（2）由题意知的所有取值为
则：
，
，
，
的分布列为:
| 2 | 4 | 5 |
|
|
|
|
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】“有黑扫黑、无黑除恶、无恶治乱”，维护社会稳定和和平发展.扫黑除恶期间，大量违法分子主动投案，某市公安机关对某月连续7天主动投案的人员进行了统计，
表示第
天主动投案的人数，得到统计表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
（1）若与具有线性相关关系，请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）判定变量与之间是正相关还是负相关.（写出正确答案，不用说明理由）
（3）预测第八天的主动投案的人数（按四舍五入取到整数）.
参考公式：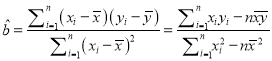
， 
.
