题目内容
【题目】已知椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆C上,且
在椭圆C上,且![]() ⊥
⊥![]()
![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l与椭圆C交于A,B两点,![]() ,若直线l始终与圆
,若直线l始终与圆![]() 相切,求半径r的值.
相切,求半径r的值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)由椭圆离心率为![]() ,点M在椭圆C上,且MF2⊥F1F2,△F1MF2的面积为
,点M在椭圆C上,且MF2⊥F1F2,△F1MF2的面积为![]() ,列出方程组求出a,b,由此能求出椭圆C的方程.
,列出方程组求出a,b,由此能求出椭圆C的方程.
(2)设直线l的方程为y=kx+m,代入椭圆方程式,得(4k2+1)x2+8kmx+4m2﹣4=0,由此利用韦达定理、根的判别式、点到直线的距离公式能求出半径的r的值.
(1)设![]() ,由题意得
,由题意得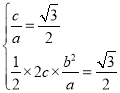
∴![]() ,
,![]()
故椭圆C的方程为![]() .
.
(2)当直线l的斜率存在时,设其直线方程为![]() ,设A(
,设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
联立方程组![]() ,整理得
,整理得![]() ,
,
由方程的判别式△=64k2m2﹣4(4k2+1)(4m2﹣4)>0,
得![]() (1)
(1)
![]() ,
,![]() ,由∠AOB=90°,得
,由∠AOB=90°,得![]()
即![]()
而![]() ,则
,则![]()
∴![]()
整理得![]()
把![]() 代入(1)得
代入(1)得![]() .
.
而![]() ,∴
,∴![]() ,显然满足
,显然满足![]() ,
,
直线l始终与圆![]() 相切,得圆心(0,0)到直线l的距离d=r,
相切,得圆心(0,0)到直线l的距离d=r,
则![]() ,
,
由![]() ,得
,得![]()
∵![]() ,∴
,∴![]() .
.
当直线l的斜率不存在时,若直线l与圆![]() 相切,此时直线l的方程为
相切,此时直线l的方程为![]() .
.
∴![]()
综上所述:![]() .
.

【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(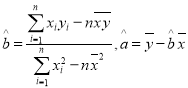 )
)
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?