ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÄłŃ§ĐŁÎȘÁËÁËœâѧÉúÊčÓĂÊÖ»ú”ÄÇéżöŁŹ·Ö±đÔÚžßÒ»ș͞߶țÁœžöÄꌶžśËæ»úłéÈĄÁË100ĂûѧÉúœűĐĐ”śČé.ÏÂĂæÊÇžùŸĘ”śČéœáčû»æÖÆ”ÄѧÉúÈŐŸùÊčÓĂÊÖ»úʱŒä”ÄÆ”Êę·ÖČŒ±íșÍÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹœ«ÊčÓĂÊÖ»úʱŒäČ»”ÍÓÚ80·ÖÖÓ”ÄѧÉúłÆÎȘĄ°ÊÖ»úĂÔĄ±.
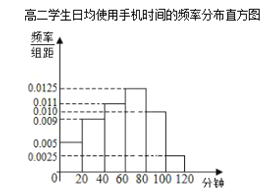
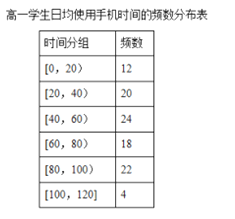
ŁšIŁ©œ«Æ”ÂÊÊÓÎȘžĆÂÊŁŹčÀŒÆÄÄžöÄꌶ”ÄѧÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊŽóŁżÇë˔ÜÀíÓÉ.
ŁšIIŁ©Ôڞ߶ț”ÄłéČéÖĐŁŹÒŃÖȘËæ»úłé”œ”ÄĆźÉúčČÓĐ55ĂûŁŹÆäÖĐ10ĂûÎȘĄ°ÊÖ»úĂÔĄ±.žùŸĘÒŃÖȘÌőŒțÍêłÉÏÂĂæ”Ä2ĄÁ2ÁĐÁȘ±íŁŹČąŸĘŽËŚÊÁÏÄăÓжàŽó”Ä°ŃÎŐÈÏÎȘĄ°ÊÖ»úĂÔĄ±ÓëĐÔ±đÓĐčŰŁż
·ÇÊÖ»úĂÔ | ÊÖ»úĂÔ | șÏŒÆ | |
ÄĐ | |||
Ćź | |||
șÏŒÆ |
žœŁșËæ»ú±äÁż![]() ŁšÆäÖĐ
ŁšÆäÖĐ![]() ÎȘŃù±ŸŚÜÁżŁ©.
ÎȘŃù±ŸŚÜÁżŁ©.
ČÎżŒÊęŸĘ |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
ĄŸŽđ°žĄżŁšąńŁ©žßÒ»ÄꌶŁŹÀíÓÉŒûœâÎöŁ»ŁšąòŁ©ÁĐÁȘ±íŒûœâÎöŁŹ90%
ĄŸœâÎöĄż
ŁšąńŁ©žùŸĘÆ”Êę·ÖČŒ±íșÍÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹ·Ö±đŒÆËăÁœžöÄêŒ¶Ń§ÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊŁŹŒŽżÉ±ÈœÏŁŹŚśłöĆжÏ.
ŁšąòŁ©žùŸĘÌâÒ⣏ÇółöÊÖ»úĂÔÈËÊęșÍ·ÇÊÖ»úĂÔÈËÊ꣏ÍêÉÆÁĐÁȘ±íŁŹŒŽżÉÓɶÀÁąĐÔŒìŃé”Äč«ÊœÇó”Ă![]() ŁŹœű¶űŚśłöĆĐ¶ÏŒŽżÉ.
ŁŹœű¶űŚśłöĆĐ¶ÏŒŽżÉ.
ŁšąńŁ©ÓÉÆ”Êę·ÖČŒ±íżÉÖȘŁŹžßÒ»Ń§ÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊÎȘ![]()
ÓÉÆ”ÂÊ·ÖČŒÖ±·œÍŒżÉÖȘŁŹžß¶țѧÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊÎȘ![]() =Łš0.0025+0.010Ł©ĄÁ20=0.25
=Łš0.0025+0.010Ł©ĄÁ20=0.25
ÒòÎȘP1![]() P2ŁŹËùÒÔžßÒ»Äꌶ”ÄѧÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊŽó.
P2ŁŹËùÒÔžßÒ»Äꌶ”ÄѧÉúÊÇĄ°ÊÖ»úĂÔĄ±”ÄžĆÂÊŽó.
ŁšąòŁ©ÓÉÆ”ÂÊ·ÖČŒÖ±·œÍŒżÉÖȘŁŹÔÚłéÈĄ”Ä100ÈËÖĐŁŹ
Ą°ÊÖ»úĂÔĄ±ÓĐŁš0.010+0.0025Ł©ĄÁ20ĄÁ100=25ŁšÈËŁ©ŁŹ
·ÇÊÖ»úĂÔÓĐ100©25=75ŁšÈËŁ©.
ŽÓ¶ű2ĄÁ2ÁĐÁȘ±íÈçÏÂŁș
·ÇÊÖ»úĂÔ | ÊÖ»úĂÔ | șÏŒÆ | |
ÄĐ | 30 | 15 | 45 |
Ćź | 45 | 10 | 55 |
șÏŒÆ | 75 | 25 | 100 |
œ«2ĄÁ2ÁĐÁȘ±íÖĐ”ÄÊęŸĘŽúÈëč«ÊœŒÆË㣏
”Ă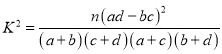
![]()
œáșÏČÎżŒÊęŸĘŁŹżÉÖȘ3.030![]() 2.706ŁŹËùÒÔÓĐ90%”Ä°ŃÎŐÈÏÎȘĄ°ÊÖ»úĂÔĄ±ÓëĐÔ±đÓĐčŰ.
2.706ŁŹËùÒÔÓĐ90%”Ä°ŃÎŐÈÏÎȘĄ°ÊÖ»úĂÔĄ±ÓëĐÔ±đÓĐčŰ.

ĄŸÌâÄżĄżÈ«ÍűŽ«Č„”ÄÈÚșÏÖžÊęÊÇșâÁż”çÊÓĂœÌćÔÚÖĐčúÍűĂńÖĐÓ°ÏìÁŠ”ÄŚÛșÏÖž±êŁŹžùŸĘÏàč۱š”ÀÌáč©”ÄÈ«ÍűŽ«Č„2018ÄêÄłÈ«čúĐÔŽóĐͻ”ÄĄ°ÊĄŒ¶ÎÀÊÓĐÂÎĆÌšĄ±ÈÚșÏÖžÊę”ÄÊęŸĘŁŹ¶ÔĂûÁĐÇ°20Ăû”ÄĄ°ÊĄŒ¶ÎÀÊÓĐÂÎĆÌšĄ±”ÄÈÚșÏÖžÊęœűĐĐ·ÖŚéÍłŒÆŁŹœáčûÈç±íËùÊŸ.
ŚéșĆ | ·ÖŚé | Æ”Êę |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
ÏÖŽÓÈÚșÏÖžÊęÔÚ![]() șÍ
șÍ![]() Äڔĥ°ÊĄŒ¶ÎÀÊÓĐÂÎĆÌšĄ±ÖĐËæ»úłéÈĄ2ŒÒœűĐĐ”śŃĐŁŹÇóÖÁÉÙÓĐ1ŒÒ”ÄÈÚșÏÖžÊęÔÚ
Äڔĥ°ÊĄŒ¶ÎÀÊÓĐÂÎĆÌšĄ±ÖĐËæ»úłéÈĄ2ŒÒœűĐĐ”śŃĐŁŹÇóÖÁÉÙÓĐ1ŒÒ”ÄÈÚșÏÖžÊęÔÚ![]() ÄڔĞĆÂÊ.
ÄڔĞĆÂÊ.