题目内容
【题目】已知定义在R上的函数![]() 对任意实数
对任意实数![]() 都满足
都满足![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断函数![]() 的单调性,并证明;
的单调性,并证明;
(3)解不等式![]() .
.
【答案】(1)![]() 为奇函数.证明见解析(2)
为奇函数.证明见解析(2)![]() 在R上为增函数.证明见解析(3)当
在R上为增函数.证明见解析(3)当![]() 时不等式的解集是
时不等式的解集是![]() .当
.当![]() 时不等式的解集是
时不等式的解集是![]() .当
.当![]() 时不等式的解集是
时不等式的解集是![]() .
.
【解析】
(1)用赋值法求出![]() ,然后令
,然后令![]() 可得奇偶性;
可得奇偶性;
(2)利用单调性的定义证明单调性;
(3)由奇函数性质化不等式为![]() ,由单调性转化为二次不等式,再分类得出解集.
,由单调性转化为二次不等式,再分类得出解集.
(1)解:![]() 为奇函数.
为奇函数.
证明:因为![]() ,令
,令![]() ,
,
得![]() 对任意的
对任意的![]() 都成立,所以
都成立,所以![]() .
.
又令![]() ,则
,则![]() ,
,
所以![]() ,所以
,所以![]() 是奇函数.
是奇函数.
(2)解:![]() 在R上为增函数.
在R上为增函数.
证明:![]() ,且使
,且使![]() 由
由![]() 是奇函数,
是奇函数,
得![]() .
.
因为当![]() 时,
时,![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 在R上为增函数.
在R上为增函数.
(3)解:由![]() ,得
,得![]() .
.
因为![]() 是奇函数,所以
是奇函数,所以![]() .
.
又![]() 在R上为增函数,所以
在R上为增函数,所以![]() .
.
即![]() ,所以
,所以![]() .
.
所以当![]() 时不等式的解集是
时不等式的解集是![]() .
.
当![]() 时不等式的解集是
时不等式的解集是![]() .
.
当![]() 时不等式的解集是
时不等式的解集是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司在过去几年内使用某种型号的灯管1 000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组 |
|
|
|
|
频数 | 48 | 121 | 208 | 223 |
频率 | ||||
分组 |
|
|
| |
频数 | 193 | 165 | 42 | |
频率 |
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.
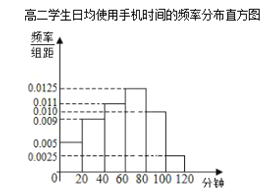
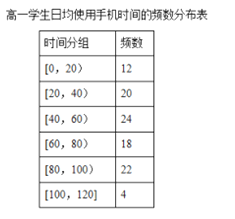
(I)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(II)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| span>2.072 | 2.706 | 3.841 | 5.024 |
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁).其猜对歌曲名称与否的人数如图所示.
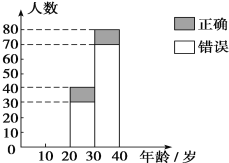
(1)写出2×2列联表;判断能否在犯错误的概率不超过0.10的前提下认为猜对歌曲名称与年龄有关系,说明你的理由.(下面的临界值表供参考)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,求20~30岁与30~40岁各有几人.
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.