题目内容
某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数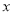 与骑兵个数
与骑兵个数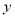 表示每天的利润
表示每天的利润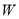 (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
题目内容
某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数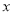 与骑兵个数
与骑兵个数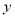 表示每天的利润
表示每天的利润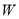 (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
 教材全解字词句篇系列答案
教材全解字词句篇系列答案