题目内容
已知等差数列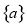 的前
的前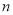 项和为
项和为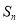 ,公差为
,公差为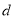 ,且
,且 ,则“
,则“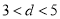 ”是“
”是“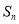 的最小值仅为
的最小值仅为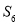 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
题目内容
已知等差数列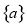 的前
的前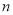 项和为
项和为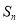 ,公差为
,公差为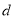 ,且
,且 ,则“
,则“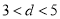 ”是“
”是“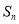 的最小值仅为
的最小值仅为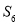 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案