题目内容
【题目】设
为抛物线
的准线上一点，F为C 的焦点，点P在C上且满足
，若当m取得最小值时，点P恰好在以原点为中心，F为焦点的双曲线上，则该双曲线的离心率为
A. 
B. 3 C. 
D. 
【答案】B
【解析】分析：由题意首先确定抛物线的方程，然后结合几何关系将原问题转化为直线与抛物线相切的问题，最后求解双曲线的离心率即可.
详解：
为抛物线
的准线上一点,
则
，解得p=6；
∴抛物线的标准方程为y2=12x，焦点为F(3,0)，准线方程为x=3；
过点P作准线的垂线，垂足为N，则由抛物线的定义可得|PN|=|PF|,
∵|PF|=m|PA|，∴|PN|=m|PA|,∴
；
如图所示，
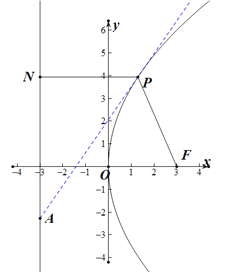
设PA的倾斜角为
，则
，
当m取得最小值时，
最小，此时直线PA与抛物线相切；
设直线PA的方程为
,代入y2=12x，
可得
.
∴
，
解得
或
(不合题意，舍去)，
可得切点
；
由题意可得双曲线的焦点为(3,0),(3,0)，
∴双曲线的实轴长为
.
∴双曲线的离心率为
.
本题选择B选项.
练习册系列答案
科学实验活动册系列答案
相关题目
