题目内容
【题目】如图所示,已知长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
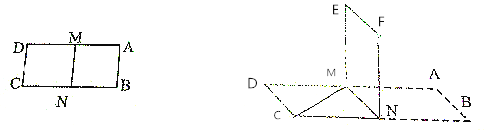
(1)求证:直线CM⊥面DFN;
(2)求点C到平面FDM的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)推导出DN⊥CM,CM⊥FN,由此能证明CM⊥平面DFN.(2)以M为原点,MN为x轴,MA为y轴,ME为z轴,建立空间直角坐标系,利用向量法能求出点C到平面FDM的距离.
证明:(1)∵长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,
将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
∴DN⊥CM,CM⊥FN,
又DN∩FN=N,∴CM⊥平面DFN.
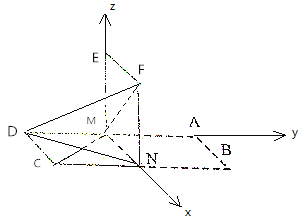
解:(2)以M为原点,MN为x轴,MA为y轴,ME为z轴,建立空间直角坐标系,
则C(2,-2,0),D(0,-2,0),F(2,0,2),M(0,0,0),![]() =(2,-2,0),
=(2,-2,0),![]() =(0,-2,0),
=(0,-2,0),![]() =(2,0,2),
=(2,0,2),
设平面FDM的法向量![]() =(x,y,z),
=(x,y,z),
则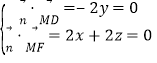 ,取x=1,得
,取x=1,得![]() =(1,0,-1),
=(1,0,-1),
∴点C到平面FDM的距离d=![]() =
=![]() =
=![]() .
.

【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)
男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
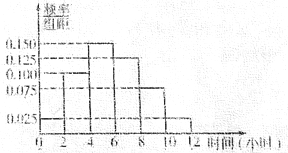
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |