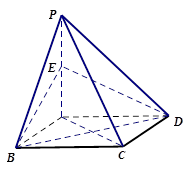
题目内容
把正方形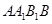 以边
以边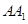 所在直线为轴旋转
所在直线为轴旋转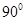 到正方形
到正方形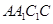 ,其中
,其中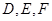 分别为
分别为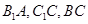 的中点.
的中点.
(1)求证: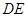 ∥平面
∥平面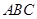 ;
;
(2)求证: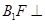 平面
平面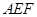 ;
;
(3)求二面角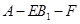 的大小.
的大小.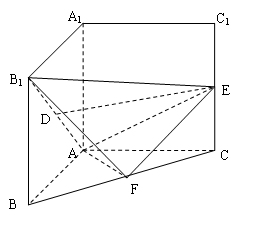
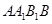 以边
以边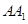 所在直线为轴旋转
所在直线为轴旋转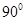 到正方形
到正方形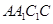 ,其中
,其中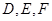 分别为
分别为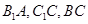 的中点.
的中点.(1)求证:
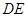 ∥平面
∥平面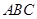 ;
;(2)求证:
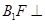 平面
平面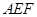 ;
;(3)求二面角
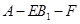 的大小.
的大小.
(1)、(2)见解析;(3)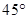 .
.
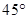 .
.本试题主要是考查了空间立体几何中,线面平行的判定和线面垂直的判定以及运用空间向量法,或者几何法求解二面角的综合试题。熟练掌握线面平行和垂直度判定定理和性质定理,是解决该试题的关键。另外求解二面角的思路一般可以借助于三垂线定理来完成。
解:(1)设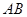 的中点为
的中点为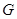 ,连接
,连接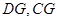
∵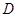 是
是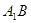 的中点∴
的中点∴ ∥
∥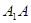 且
且
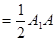 ……………(2分)
……………(2分)
∵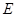 是
是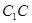 的中点∴
的中点∴ ∥
∥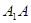 且
且
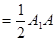 ,∴
,∴ ∥
∥ 且
且
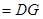
∴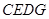 是平行四边形,∴
是平行四边形,∴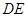 ∥
∥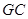
∵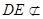 平面
平面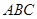 ,
,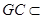 平面
平面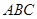 ,∴
,∴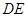 ∥平面
∥平面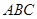 ……………(4分)
……………(4分)
(2) ∵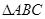 为等腰直角三角形,
为等腰直角三角形,  ,且
,且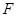 是
是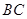 的中点
的中点
∴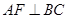 ∵平面
∵平面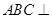 平面
平面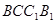 ∴
∴  平面
平面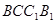
∴
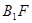 ………………(6分)
………………(6分)
设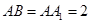 ,则在
,则在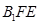 中,
中,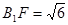 ,
,
则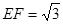 ,
, ∴
∴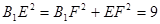
∴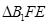 是直角三角形,∴
是直角三角形,∴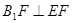
∵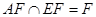 ∴
∴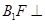 平面
平面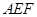 …(8分)
…(8分)
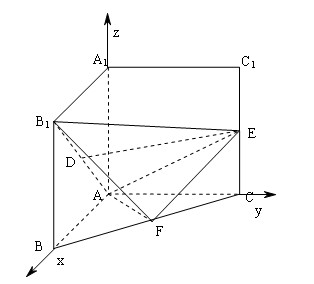
(3)分别以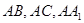 为
为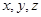 轴建立空间直角坐标系
轴建立空间直角坐标系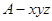 如图,
如图,
设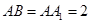 ,则设
,则设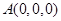 ,
,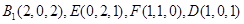 ………(9分)
………(9分)
∵ 平面
平面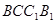 ,∴ 面
,∴ 面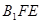 的法向量为
的法向量为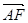 =
=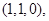 ……………(10分)
……………(10分)
设平面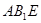 的法向量为
的法向量为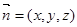 ,∵
,∵ 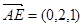 ,
, 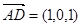
∴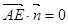 ,
, 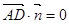 , ∴
, ∴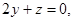 ,
,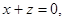
不妨设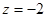 ,可得
,可得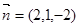 ………………(11分)
………………(11分)
,∴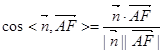 =
=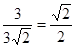
∵ 二面角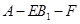 是锐角,∴ 二面角
是锐角,∴ 二面角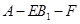 的大小
的大小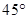 ..........(12分)
..........(12分)
解:(1)设
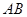 的中点为
的中点为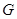 ,连接
,连接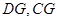
∵
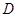 是
是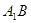 的中点∴
的中点∴ ∥
∥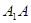 且
且
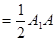 ……………(2分)
……………(2分)∵
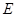 是
是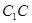 的中点∴
的中点∴ ∥
∥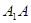 且
且
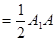 ,∴
,∴ ∥
∥ 且
且
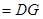
∴
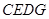 是平行四边形,∴
是平行四边形,∴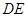 ∥
∥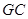
∵
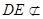 平面
平面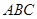 ,
,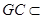 平面
平面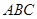 ,∴
,∴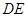 ∥平面
∥平面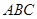 ……………(4分)
……………(4分)(2) ∵
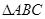 为等腰直角三角形,
为等腰直角三角形,  ,且
,且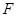 是
是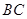 的中点
的中点 ∴
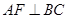 ∵平面
∵平面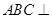 平面
平面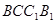 ∴
∴  平面
平面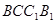
∴

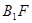 ………………(6分)
………………(6分) 设
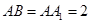 ,则在
,则在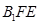 中,
中,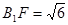 ,
,则
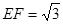 ,
, ∴
∴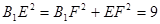
∴
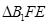 是直角三角形,∴
是直角三角形,∴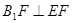
∵
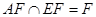 ∴
∴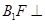 平面
平面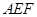 …(8分)
…(8分) (3)分别以
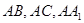 为
为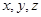 轴建立空间直角坐标系
轴建立空间直角坐标系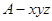 如图,
如图,
设
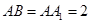 ,则设
,则设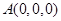 ,
,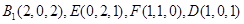 ………(9分)
………(9分)∵
 平面
平面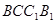 ,∴ 面
,∴ 面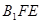 的法向量为
的法向量为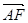 =
=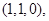 ……………(10分)
……………(10分)设平面
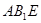 的法向量为
的法向量为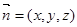 ,∵
,∵ 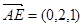 ,
, 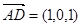
∴
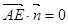 ,
, 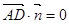 , ∴
, ∴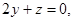 ,
,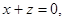
不妨设
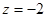 ,可得
,可得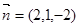 ………………(11分)
………………(11分),∴
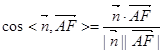 =
=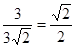
∵ 二面角
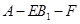 是锐角,∴ 二面角
是锐角,∴ 二面角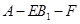 的大小
的大小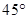 ..........(12分)
..........(12分)
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
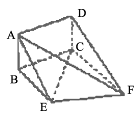
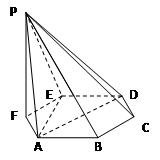
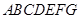 为多面体,平面
为多面体,平面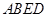 与平面
与平面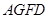 垂直,点
垂直,点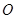 在线段
在线段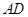 上,
上,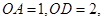 △OAB,,△
△OAB,,△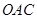 ,△
,△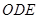 ,△
,△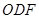 都是正三角形。
都是正三角形。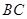 ∥
∥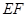 ;
;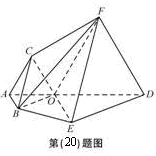
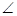 BCF=
BCF=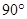 ,AD=
,AD=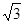 ,EF=2.
,EF=2.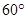 .
.
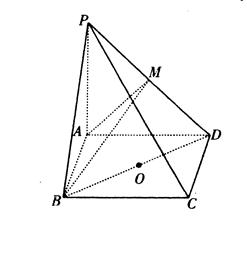
 中,已知点
中,已知点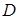 、
、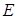 、
、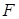 分别为棱
分别为棱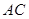 、
、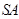 、
、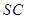 的中点.
的中点. ∥平面
∥平面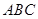 ;
;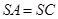 ,
,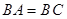 ,求证:平面
,求证:平面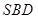 ⊥平面
⊥平面
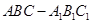 中,
中,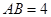 ,
,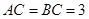 ,
,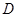 为
为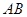 的中点。(Ⅰ)求点C到平面
的中点。(Ⅰ)求点C到平面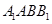 的距离;(Ⅱ)若
的距离;(Ⅱ)若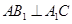 ,求二面角
,求二面角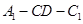 的平面角的余弦值。
的平面角的余弦值。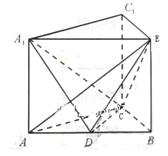
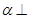 平面
平面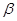 ,那么平面
,那么平面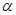 内一定存在直线平行于平面
内一定存在直线平行于平面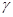 ,平面
,平面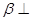 平面
平面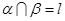 ,那么
,那么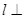 平面
平面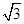 , 点P为矩形ABCD所
, 点P为矩形ABCD所