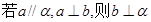题目内容
如图,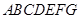 为多面体,平面
为多面体,平面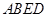 与平面
与平面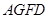 垂直,点
垂直,点 在线段
在线段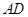 上,
上,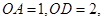 △OAB,,△
△OAB,,△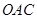 ,△
,△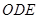 ,△
,△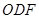 都是正三角形。
都是正三角形。
(Ⅰ)证明直线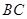 ∥
∥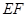 ;
;
(II)求棱锥F—OBED的体积。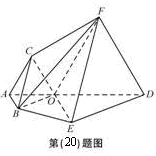
 为多面体,平面
为多面体,平面 与平面
与平面 垂直,点
垂直,点 在线段
在线段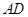 上,
上,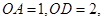 △OAB,,△
△OAB,,△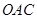 ,△
,△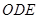 ,△
,△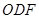 都是正三角形。
都是正三角形。(Ⅰ)证明直线
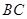 ∥
∥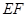 ;
;(II)求棱锥F—OBED的体积。

(1)见解析;(2)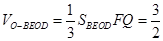
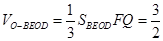
第一问中运用线面平行的性质定理,可以求证线线平行,结合了三角形的中位线定理。第二问中,求解棱锥的体积问题,一般就是求解底面积和高即可。先建立空间直角坐标系,然后表示三角形的面积,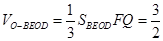 ,
,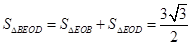 ,结合向量的关系式得到体积公式。
,结合向量的关系式得到体积公式。
解:
(I)(综合法)
证明:设G是线段DA与EB延长线的交点. 由于△OAB与△ODE都是正三角形,所以
OB∥1/2DE,OB =1/2DE,OG=OD=2, 同理,设G’是线段DA与线段FC延长线的交点,有OG’=OD=2
又由于G和G’都在线段DA的延长线上,所以G与G’重合.
在△GED和△GFD中,由
OB∥1/2DE,OB =1/2DE和OC∥1/2DF,OC=1/2DF可知B和C分别是GE和GF的中点,所以BC是△GEF的中位线,故BC∥EF.
(向量法)
过点F作FQ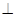 AD,交AD于点Q,连QE,由平面ABED⊥平面ADFC,知FQ⊥平面ABED,以Q为坐标原点,QE为X轴正向,QD为y轴正向,DF为z轴正向,建立如图所示空间直角坐标系.
AD,交AD于点Q,连QE,由平面ABED⊥平面ADFC,知FQ⊥平面ABED,以Q为坐标原点,QE为X轴正向,QD为y轴正向,DF为z轴正向,建立如图所示空间直角坐标系.
由条件知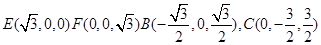
则有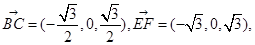
所以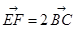 即得BC∥EF.
即得BC∥EF.
(II)解:由OB=1,OE=2, ,而△OED是边长为2的正三角形,故
,而△OED是边长为2的正三角形,故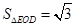
所以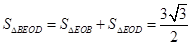
过点F作FQ⊥AD,交AD于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F—OBED的高,且FQ=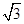 ,所以
,所以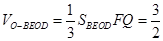
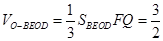 ,
,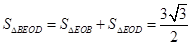 ,结合向量的关系式得到体积公式。
,结合向量的关系式得到体积公式。解:
(I)(综合法)
证明:设G是线段DA与EB延长线的交点. 由于△OAB与△ODE都是正三角形,所以
|
又由于G和G’都在线段DA的延长线上,所以G与G’重合.
在△GED和△GFD中,由
|
(向量法)
过点F作FQ
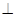 AD,交AD于点Q,连QE,由平面ABED⊥平面ADFC,知FQ⊥平面ABED,以Q为坐标原点,QE为X轴正向,QD为y轴正向,DF为z轴正向,建立如图所示空间直角坐标系.
AD,交AD于点Q,连QE,由平面ABED⊥平面ADFC,知FQ⊥平面ABED,以Q为坐标原点,QE为X轴正向,QD为y轴正向,DF为z轴正向,建立如图所示空间直角坐标系.由条件知
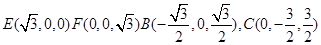
则有
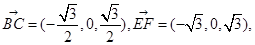
所以
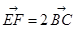 即得BC∥EF.
即得BC∥EF.(II)解:由OB=1,OE=2,
 ,而△OED是边长为2的正三角形,故
,而△OED是边长为2的正三角形,故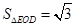
所以
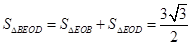
过点F作FQ⊥AD,交AD于点Q,由平面ABED⊥平面ACFD知,FQ就是四棱锥F—OBED的高,且FQ=
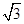 ,所以
,所以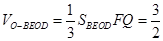

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
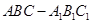 中,
中,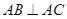 ,
,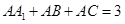 ,
,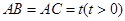 ,
,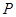 是侧棱
是侧棱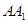 上的动点.
上的动点.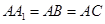 时,求证:
时,求证: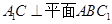 ;
; 的平面角的余弦值为
的平面角的余弦值为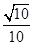 ,试求实数
,试求实数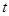 的值.
的值.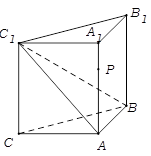
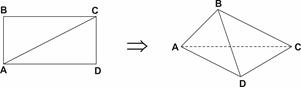
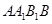 以边
以边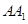 所在直线为轴旋转
所在直线为轴旋转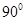 到正方形
到正方形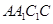 ,其中
,其中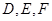 分别为
分别为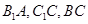 的中点.
的中点.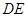 ∥平面
∥平面 ;
; 平面
平面 ;
;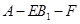 的大小.
的大小.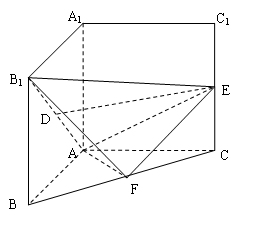
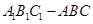 中,
中, 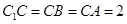 ,
, .
. 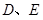 分别为棱
分别为棱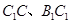 的中点.
的中点.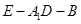 的平面角的余弦值;
的平面角的余弦值;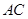 上是否存在一点
上是否存在一点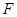 ,使得
,使得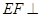 平
平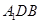 ?
?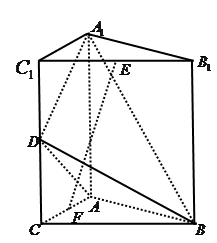
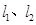 为异面直线,直线
为异面直线,直线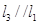 ,则
,则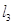 与
与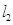 的位置关系是
的位置关系是 中,底面
中,底面 为矩形,平面
为矩形,平面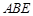 ,
,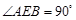 ,
,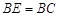 ,
,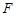 为
为 的中点,
的中点,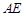 ∥平面
∥平面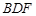 ;(2)平面
;(2)平面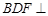 平面
平面 .
.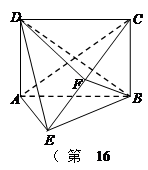
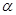 ,
,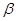 ,直线a,b,给出以下命题,正确的是( )
,直线a,b,给出以下命题,正确的是( )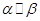
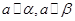 ,且a不在
,且a不在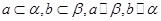 ,则
,则 ,有以下几个命题,其中是真命题的序号为 。(1)若
,有以下几个命题,其中是真命题的序号为 。(1)若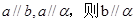 (2)
(2)
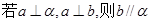 (4)
(4)