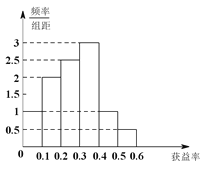
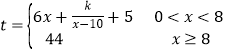题目内容
【题目】在平面直角坐标系中,![]() ,
,![]() ,
,![]() (O是坐标原点),其中
(O是坐标原点),其中![]() 。
。
(1)求B点坐标;
(2)求四边形OABC在第一象限部分面积![]() .
.
【答案】(1)![]() .
.
(2)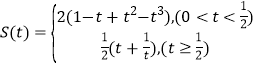 .
.
【解析】
分析:(1)利用向量的加法运算,表示出![]() ,再根据OABC为矩形的特征,表示出B点坐标。
,再根据OABC为矩形的特征,表示出B点坐标。
(2)讨论当t取不同值时(也就是B点坐标在第一象限或第二象限),四边形OABC落在第一象限内的面积。当点B在第一象限时,落在第一象限内的部分为直角梯形,可用整个面积减去第二象限面积的方法求得;当B在第二象限时,落在第一象限内的部分为直角三角形,可以直接求得。最后结果写成分段函数的形式。
详解:(1)∵![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
又∵![]() ,∴
,∴![]() ,
,
∴![]() 为矩形,
为矩形,
∵![]() ,
,
∴![]()
(2)①当![]() ,即
,即![]() 时,
时,![]() 在第一象限,
在第一象限,![]() 在第一象限,
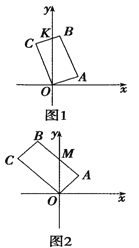
在第一象限,![]() 在第二象限(如图1),此时
在第二象限(如图1),此时![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() 交
交![]() 轴于
轴于![]()
![]() ,
,
∴![]()
②当![]() ,即
,即![]() 时,
时,![]() 在第一象限,
在第一象限,![]() 在
在![]() 轴上或在第二象限,
轴上或在第二象限,![]() 在第二象限(如图2),此时
在第二象限(如图2),此时![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() 交
交![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴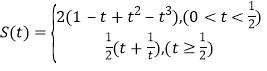 .
.

练习册系列答案
相关题目