题目内容
2.过抛物线C:y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为坐标原点,|AB|=8p,且S△AOB=4,则p的值为( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 设出过抛物线C焦点F的直线方程以及直线与抛物线的交点坐标,由|AB|=|AF|+|BF|=8p,求出直线AB的方程,再由△AOB的面积求出p的值.
解答 解:∵抛物线C:y2=2px(p>0)的焦点为F($\frac{p}{2}$,0),
∴设过抛物线C焦点F的直线方程为:y=k(x-$\frac{p}{2}$),
且直线l交抛物线于A(x1,y1)、B(x2,y2)两点,
∴|AB|=|AF|+|BF|=(x1+$\frac{p}{2}$)+(x2+$\frac{p}{2}$)=x1+x2+p=8p,
∴x1+x2=7p;
又直线与抛物线联立,得$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=k(x-\frac{p}{2})}\end{array}\right.$,
消去y,得k2x2-(k2+2)px+$\frac{{p}^{2}}{4}$=0,
∴x1+x2=$\frac{{(k}^{2}+2)p}{{k}^{2}}$;
即$\frac{{(k}^{2}+2)p}{{k}^{2}}$=7p,
∴k2=$\frac{1}{3}$,
不妨取k=$\frac{1}{\sqrt{3}}$;
则原点O到直线AB:kx-y-$\frac{kp}{2}$=0的距离为
d=$\frac{\frac{kp}{2}}{\sqrt{{k}^{2}+1}}$=$\frac{\frac{p}{2\sqrt{3}}}{\sqrt{\frac{1}{3}+1}}$=$\frac{p}{4}$,且|AB|=8p,
∴△AOB的面积为
S△AOB=$\frac{1}{2}$•d•|AB|=$\frac{1}{2}$•$\frac{p}{4}$•8p=4,
解得p=±2,应取p的值为2.
故选:B.
点评 本题考查了直线与抛物线的应用问题,也考查了方程组思想以及根与系数的应用问题,考查了三角形面积的计算问题,是综合性题目.

| A. | log22015 | B. | 2015 | C. | -2015 | D. | 1008 |
| A. | $({\frac{7π}{12},0})$ | B. | $({\frac{π}{3},0})$ | C. | $({\frac{11π}{6},0})$ | D. | $({\frac{3π}{2},0})$ |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
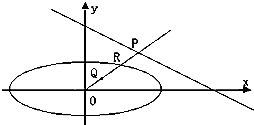 已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.
已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.