题目内容
10．已知正数x，y满足x+y=4，求$\frac{1}{x}+\frac{2}{y}$的最小值．分析 由题意可得$\frac{1}{x}+\frac{2}{y}$=$\frac{1}{4}$（$\frac{1}{x}+\frac{2}{y}$）（x+y）=$\frac{1}{4}$（3+$\frac{y}{x}$+$\frac{2x}{y}$），由基本不等式可得．
解答 解：∵正数x，y满足x+y=4，
∴$\frac{1}{x}+\frac{2}{y}$=$\frac{1}{4}$（$\frac{1}{x}+\frac{2}{y}$）（x+y）
=$\frac{1}{4}$（3+$\frac{y}{x}$+$\frac{2x}{y}$）≥$\frac{1}{4}$（3+2$\sqrt{2}$），
当且仅当$\frac{y}{x}$=$\frac{2x}{y}$即x=4（$\sqrt{2}$-1）且y=4（2-$\sqrt{2}$）时取等号，
∴$\frac{1}{x}+\frac{2}{y}$的最小值为$\frac{1}{4}$（3+2$\sqrt{2}$）
点评 本题考查基本不等式求最值，整体法是解决问题的关键，属基础题．
练习册系列答案
相关题目
8．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打时间x（单位：小时）与当于投篮命中率y之间的关系：
（Ⅰ）根据上表的数据，求出y关于x的线性回归方程y=$\widehat{b}$x+a；
（Ⅱ）预测小李该月6号打6小时篮球的投篮命中率为多少？（考点：线性回归应用）
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
（Ⅱ）预测小李该月6号打6小时篮球的投篮命中率为多少？（考点：线性回归应用）
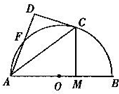如图，AB是圆O的直径，C、F为圆O上点，CA是∠BAF的角平分线，CD与圆O切于点C且交AF的延长线于点D，CM⊥AB，垂足为点M，求证：