题目内容
11.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
分析 根据题意和向量的数量积化简$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,求出向量$\overrightarrow{a},\overrightarrow{b}$的关系,再将式子$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|两边平方,化简后可求出向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:∵|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,且$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,
∴$|\overrightarrow{a}{|}^{2}+3|\overrightarrow{a}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,化简可得,$|\overrightarrow{a}|=|\overrightarrow{b}|$,
由$\sqrt{3}$|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|得,|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}$|,
两边平方可得,${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={\overrightarrow{a}}^{2}$,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$-\frac{1}{2}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{2π}{3}$,
故选:D.
点评 本题考查向量的数量积运算的综合应用,以及结论:$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}+|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=2(|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2})$,属于中档题.

 阅读快车系列答案
阅读快车系列答案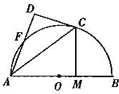 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证: