题目内容
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知2B=A+C,a+$\sqrt{2}$b=2c,求sinC的值.分析 由已知及正弦定理可得:sin(C-30°)=$\frac{\sqrt{2}}{2}$,可解得C的值,由两角和的正弦函数公式即可得解.
解答 解:由2B=A+C及180°=A+C+B,得B=60°,
因为a+$\sqrt{2}$b=2c,
所以由正弦定理可得:sinA+$\sqrt{2}$sinB=2sinC,
可得:sin(120°-C)+$\frac{\sqrt{6}}{2}$=2sinC,
解得:sin(C-30°)=$\frac{\sqrt{2}}{2}$,故C-30°=45°,
可得:C=45°+30°,
所以:sinC=sin(45°+30°)=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
点评 本题主要考查了正弦定理的应用,三角函数恒等变换的应用,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}|x+1|,-7≤x≤0\\ 1nx,{e^{-2}}≤x≤e\end{array}$,g(x)=x2-2x,设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数a的取值范围为( )
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
9.设函数f(x)满足f(x)=f(4-x)(x∈R),且当x>2时f(x)为增函数,记a=f(1.10.5),b=f(0.51.1),c=f(log0.5$\frac{1}{16}$),则a、b、c的大小关系为( )
| A. | c<b<a | B. | c<a<b | C. | b<a,c | D. | a<b<c |
7.已知函数f(x)=$\frac{1}{1-x}$,g(x)=lnx,x0是函数h(x)=f(x)+g(x)的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | h(x1)<0,h(x2)<0 | B. | h(x1)>0,h(x2)>0 | C. | h(x1)>0,h(x2)<0 | D. | h(x1)<0,h(x2)>0 |
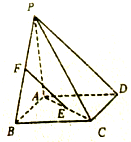 如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.
如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.