Question

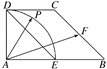
【题目】(2016·沈阳期中)在直角梯形ABCD中，AB⊥AD，DC∥AB，AD＝DC＝1，AB＝2，E、F分别为AB、BC的中点，点P在以A为圆心，AD为半径的圆弧上变动(如图所示)．若＝λ＋μ，其中λ，μ∈R，则2λ－μ的取值范围是______________.

Answer 1

【答案】[－1,1]

【解析】建立如图所示的直角坐标系，设∠PAE＝α，则

A(0,0)，E(1,0)，D(0,1)，F(1.5,0.5)，P(cosα，sin α)(0°≤α≤90°)．

∵＝λ＋μ，

∴(cosα，sin α)＝λ(－1,1)＋μ(1.5,0.5)，

∴cosα＝－λ＋1.5μ，sin α＝λ＋0.5μ，

∴λ＝ (3sin α－cosα)，μ＝ (cosα＋sin α)，

∴2λ－μ＝sin α－cosα＝sin(α－45°)．

∵0°≤α≤90°，∴－45°≤α－45°≤45°，

∴－≤sin(α－45°)≤，

∴－1≤sin(α－45°)≤1.

∴2λ－μ的取值范围是[－1,1]．